|
Chapitre
VII:
OSCILLATEUR
HARMONIQUE
|
I- DÉFINITIONS :
1-
Définition :
On appelle oscillateur
harmonique tout système mécanique ou électrique dont l'évolution (
de la position, de la vitesse ou de l'accélération) est fonction
sinusoïdale du temps (sinus ou cosinus).
Exemple :
¨
Masse fixée à l'extrémité d'un ressort.
¨
Pendule de torsion.
¨
Circuit électrique L C.
L'évolution du système est la solution générale d'une équation
différentielle du second ordre linéaire à coefficients constants du
type :
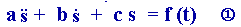
a, b, c sont des
constantes qui caractérisent le système et f (t) correspond à
l'action du milieu extérieur sur le système ( force, couple, ddp).
Si 
L'équation
 définit les mouvements propres du système dont les solutions forment
un espace vectoriel de dimension 2.
définit les mouvements propres du système dont les solutions forment
un espace vectoriel de dimension 2.
Si
(s1(t) , s2(t)) est une base, alors  est la solution générale de l'équation
est la solution générale de l'équation  .
.
La recherche des solutions de l'équation  sous la forme de
sous la forme de 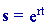 ,
montre que r doit être solution de l'équation caractéristique
associée : ,
montre que r doit être solution de l'équation caractéristique
associée :
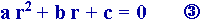
Les
racines de cette équation dépendent de la valeur du discriminant :

Solution
générale de  =
solution générale de =
solution générale de  + solution particulière de
+ solution particulière de
Remarques
:
Dans  si b = 0 et f (t) = 0 Þ
Oscillations harmoniques libres ( pures )
si b = 0 et f (t) = 0 Þ
Oscillations harmoniques libres ( pures )
Dans  si b ¹
0 et f (t) = 0 Þ
Oscillations amorties
si b ¹
0 et f (t) = 0 Þ
Oscillations amorties
Dans si b = 0 et f (t) ¹
0 Þ
Oscillations forcées
si b = 0 et f (t) ¹
0 Þ
Oscillations forcées
II-
LES OSCILLATIONS :
Modèle physique
¨
Dans une oscillation pure on a conservation d'énergie.
¨
Dans une oscillation amortie on a dissipation d'énergie.
¨
Dans une oscillation couplée on a échange d'énergie.
¨
Dans une oscillation forcée on a apport d'énergie.
Remarque :
Un pendule n'est pas un oscillateur harmonique si
l'angle q
est grand ( si q
est petit, on peut le considérer comme oscillateur harmonique).
III-
OSCILLATION HARMONIQUE :
1-
Formulation mathématique :
Si la variable s est une fonction sinusoïdale du temps
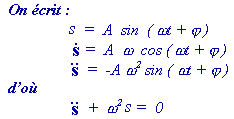
C'est
l'équation différentielle d'évolution du système :
A : amplitude > 0
s : l'élongation
w : pulsation
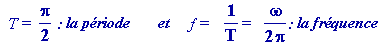
2-
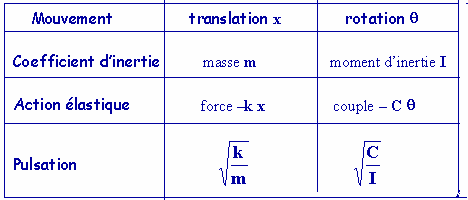
Exemples :
a-
Oscillateur rectiligne : ressort
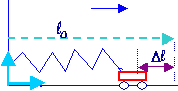
Une masse m est accrochée à une des extrémités du
ressort, on constate que le ressort exerce sur elle une force de
rappel ( donnée par la loi de Hooke) :

b- Mouvement harmonique de rotation :
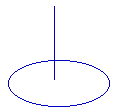
Dans
une oscillation de torsion, on a un couple de rappel proportionnel à q.
Ce couple a pour expression :
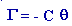
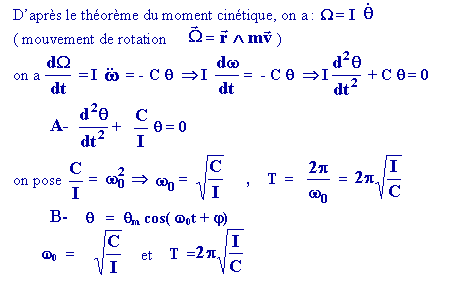
3-
Énergie mécanique d'un oscillateur harmonique :
a-
Oscillateur harmonique linéaire :

avec
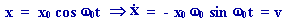
On
obtient :
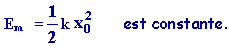
b- Oscillateur harmonique de rotation :
même
calcul, on obtient:
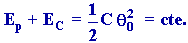
IV-
OSCILLATEUR HARMONIQUE AMORTI :
1-
Cas d'un ressort :
La masse m est soumise à son poids, à la réaction et
à la force de rappel. Mais dans la pratique d'autres forces peuvent
s'exercer sur l'oscillateur harmonique qui tend à réduire
l'amplitude des oscillations successives : ces forces s'appellent
forces d'amortissement, elles peuvent être proportionnelles à la
vitesse :




V-
OSCILLATIONS FORCÉES :
Dans le cas du ressort on applique sur la masse m, en
plus de la force de rappel et de la force d'amortissement, une force
:
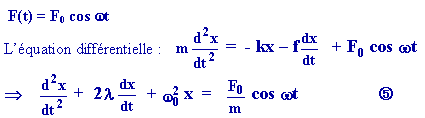

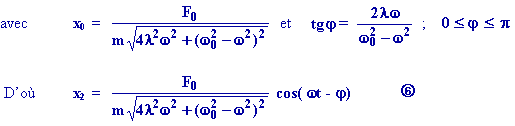
VI-
PENDULE SIMPLE: mouvement pseudo-sinusoïdal :
· On considère une masse m accrochée à un fil
inextensible et sans masse.
· On note q
l'angle du fil avec la verticale, q0
l'angle initial et v0 = 0
bilan des forces :
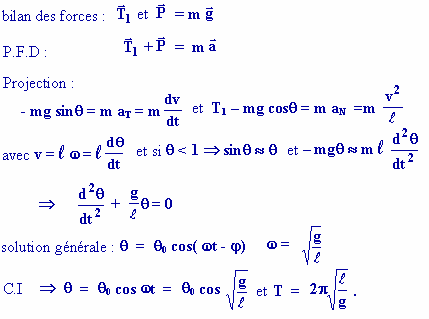
Page Suivante
|