MÉCANIQUE

I- DÉFINITIONS :

        1- Le moment d'inertie d'un point matériel de masse m par rapport à un axe (D) est défini par :
                   I = m r²          où r est la distance de la masse m à l'axe (D).
     2- Le moment d'inertie d'un solide indéformable est :
                       où r est la distance de l'élément dm à l'axe (D).

II- CALCUL DE MOMENT D'INERTIE PAR RAPPORT A UN AXE DE SYMÉTRIE :

III - ÉNERGIE CINÉTIQUE ET MOMENT CINÉTIQUE PAR RAPPORT A UN AXE FIXE :

  1- Définition :

    Soit un solide S indéformable et qui tourne à la vitesse angulaire w.
. L'énergie cinétique de rotation est :
            T = I w²          I :moment d'inertie par rapport à (D)

. Le moment cinétique est défini par :
             W = I w
. Le principe de conservation de l'énergie mécanique s'écrit ainsi :
        T + U = I w² + U = cte           U : énergie potentielle

   Théorème du moment cinétique :

        La dérivée du moment cinétique W = I w  par rapport au temps est égale aux des moments des forces qui agissant sur le solide en mouvement de rotation par rapport à (D)
2- Travail et puissance en mouvement de rotation:

        on considère un solide S en mouvement de rotation par rapport à l'axe (D), le travail élémentaire effectué par au cours de la rotation du solide d'un angle dq  est :

   IV - CENTRE DE GRAVITE :

    dans un repère quelconque (O, x, y, z)  les particules M_i de masses m_i sont repérées par les vecteurs positions :

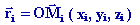
    1- Définition : Le centre d'inertie G (appelé aussi centre de masse ou centre de gravité)  de l'ensemble des points M_i est le barycentre définit par