MÉCANIQUE

THÉORÈME DE L'ÉNERGIE CINÉTIQUE :
1. Travail
         a. Travail élémentaire
          On appelle travail élémentaire effectué par une force , dont le point d'application M se déplace d'une longueur élémentaire (rectiligne ou curviligne) avec une vitesse dans le référentiel R, le produit scalaire :

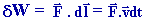
  Remarques :
- le travail est fonction du référentiel choisi.
- Il n'y a pas obligatoirement de corrélation entre la force et la cause qui provoque le déplacement.
              b. Travail fini
                   Cas général
- Le travail effectué par la force , dont le point d'application M se déplace entre le point de départ " 1 " et le point d'arrivée " 2 ", est :

- La force peut être fonction des coordonnées (u₁, u₂, u₃ ) de son point d'application M, de la vitesse et du temps.
Dans ce cas le travail dépend des positions extrêmes " 1 " et " 2 " du chemin suivi pour aller de " 1 " à " 2 " et de la loi du mouvement entre ces deux points.
- Si le vecteur force ne dépend que de la position de son point d'application M, c'est-à-dire des seules coordonnées u₁, u₂ et u₃ , on dit que M se déplace dans un champ de vecteurs forces (ou encore dans un champ de forces).
Dans ce cas le travail n'est plus fonction de la loi du mouvement mais seulement des extrémités " 1 " et " 2 " et du trajet suivi par M entre ces deux points.

         Cas d'une force conservative : 

 - On dit qu'une force 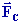(u₁, u₂, u₃ ) est conservative si le travail de cette force ne dépend pas du chemin suivi entre " 1 " et " 2 ".
 - Le long d'une courbe fermée quelconque le travail d'une force conservative est nul.

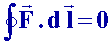
- Une force conservative dérive d'une  énergie potentielle Ep (u₁, u₂, u₃ ) telle que :
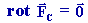  Þ  

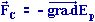
- Le travail d'une force conservative dépend uniquement du point de départ " 1 " et du point d'arrivée " 2 ".

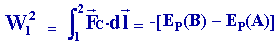
2. Énergie :
      a. Énergie potentielle d'interaction
         Définition
 L'énergie potentielle associée à la force conservative , est définie par :

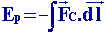
         Propriétés
- L'énergie potentielle d'interaction dépend du référentiel choisi.
- Elle est définie à une constante arbitraire près. Seules les différences d'énergie potentielle ont une signification physique.
     b. Énergie cinétique
Relativement au référentiel R, l'énergie cinétique d'un point matériel M de masse m et de quantité de mouvement à l'instant t a pour expression :

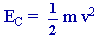
     c. Énergie mécanique totale
On appelle énergie mécanique totale E_m d'une particule M la somme de l'énergie potentielle et de l'énergie cinétique.

E_m = E_c + E_p

3. Théorème de l'énergie cinétique
      a. Cas général
- Le travail de toutes les forces " réelles " (conservatives et non conservatives) appliquées au point matériel M, dans le référentiel galiléen R, entre la position initiale " 1 " et la position finale " 2 " est égal à la variation de l'énergie cinétique de M.

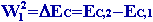
- Dans un référentiel non galiléen R', il suffit d'ajouter à å, la somme des forces d'inertie å'
     b. Cas des forces conservatives
Si les forces en présence sont conservatives, il y a conservation de l'énergie mécanique totale.

E_c + E_p  = E_m = cte

Page Suivante