|
1-Mouvements
relatifs et absolus :
Les équations horaires de la trajectoire, de la vitesse et de
l'accélération d'un mobile dépendent du système de référence
auquel est rapporté le mouvement. Soit un référentiel 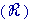 fixe
au cours du temps, fixe
au cours du temps, 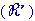 un référentiel en mouvement par rapport à
un référentiel en mouvement par rapport à 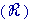 et M un point qui se déplace par rapport à
et M un point qui se déplace par rapport à 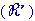 selon le schéma suivant :
selon le schéma suivant :

· Le mouvement de M par rapport à 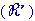 est appelé mouvement relatif.
est appelé mouvement relatif.
La trajectoire ( Cr ), la vitesse  et l'accélération
et l'accélération 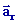 sont
toutes relatives. sont
toutes relatives.
· Le mouvement de M par rapport à 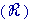 ( repère fixe) est appelé mouvement absolu.
( repère fixe) est appelé mouvement absolu.
La trajectoire ( Ca ), la vitesse 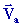 et l'accélération
et l'accélération 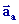 sont absolues.
sont absolues.
· Le mouvement de 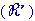 par rapport à
par rapport à 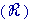 est appelé mouvement d'entraînement.
est appelé mouvement d'entraînement.
La trajectoire (Ce ), la vitesse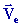 et l'accélération
et l'accélération 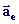 sont dites d'entraînement.
sont dites d'entraînement.
2-COMPOSITION
DES VITESSES :
Supposons que ( x, y, z ) sont les coordonnées de M
dans le repère fixe 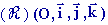 et que ( X, Y, Z ) sont les coordonnées de M dans le repère mobile
et que ( X, Y, Z ) sont les coordonnées de M dans le repère mobile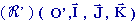
A l'instant t on a :

Si on dérive

. 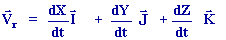 est
appelée vitesse relative et représente la vitesse du point M dans le
repère mobile est
appelée vitesse relative et représente la vitesse du point M dans le
repère mobile 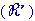
.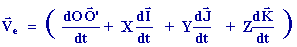 est
appelée vitesse d'entraînement et représente la vitesse du repère
mobile est
appelée vitesse d'entraînement et représente la vitesse du repère
mobile 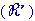 par rapport au repère fixe
par rapport au repère fixe 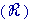 (
méthode du point coïncidant dont les coordonnées X, Y, et Z sont
constants dans le temps ) (
méthode du point coïncidant dont les coordonnées X, Y, et Z sont
constants dans le temps )
THÉORÈME
DE COMPOSITION DES VITESSES :
Le vecteur vitesse absolue est égal à la somme des vecteurs vitesses
relative et d'entraînement .
3-
COMPOSITION DES ACCÉLÉRATIONS :
Si on dérive le vecteur vitesse absolue par rapport au temps, on
obtient le vecteur accélération absolue 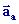 définit dans le repère
définit dans le repère 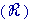 : :

· 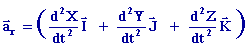 est l'accélération du point M par rapport au repère mobile
est l'accélération du point M par rapport au repère mobile 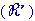 ou accélération relative
ou accélération relative
·  est
l'accélération d'entraînement qui représente l'accélération du
repère mobile est
l'accélération d'entraînement qui représente l'accélération du
repère mobile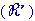 par rapport au repère fixe
par rapport au repère fixe 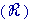 (
méthode du point coïncidant dont les coordonnées X, Y, et Z sont
constants dans le temps ) (
méthode du point coïncidant dont les coordonnées X, Y, et Z sont
constants dans le temps )
· 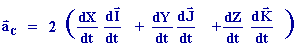 est l'accélération complémentaire ou l'accélération de Coriolis.
est l'accélération complémentaire ou l'accélération de Coriolis.
THÉORÈME
DE COMPOSITION DES ACCÉLÉRATIONS :
Le
vecteur accélération absolue est égal à la somme des vecteurs
accélérations relative, d'entraînement et de Coriolis :
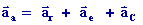
On
démontre aussi que

Page Suivante
|