|
IV-
COORDONNÉES POLAIRES OU SEMI-POLAIRES
On
introduit l'opérateur vectoriel différentiel appelé nabla ou del défini
par
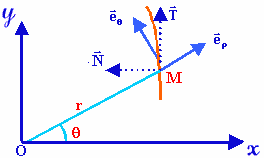
En coordonnées polaires, la position de M est repérée par le rayon
vecteur OM de module r
( t ) et par l'angle polaire q
( t ) qui peuvent varier en fonction du temps :
x = r
cos q
y = r
sin q
Pour un déplacement élémentaire, on doit avoir deux
accroissements dr
et dq
L'élément de surface est égal à rdr
dq.
On définit les vecteurs unitaires (
,
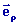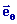) et dans la base (
,
 )
:
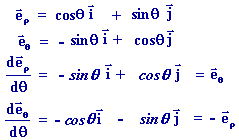
Dans la base des coordonnées polaires (
,
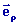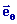), le vecteur position s'écrit
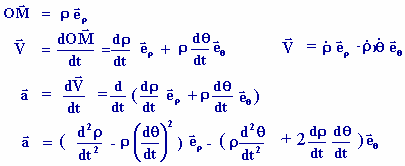
Remarque
: Les accélérations radiale et orthoradiale sont
différentes de celles normale et orthonormale.
Page Suivante
| 
