|
Chapitre
1:
RAPPELS
MATHÉMATIQUES
|
I -
LES UNITÉS

II- LES VECTEURS : rappels et définitions
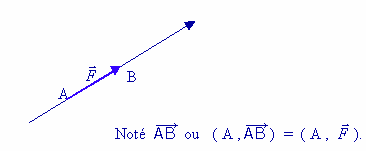
1 - Définition : un vecteur est une portion de droite limitée par deux points A et B. Dans le cas d’une force, il se caractérise par :
· son origine qui est son point d’application.
· son intensité qui est son module.
· le support qui est la droite.
· le sens.
2 - Projection et
coordonnées :


 
· Projection d’un vecteur sur une droite :
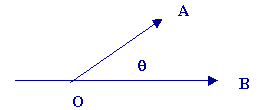
La projection d’un vecteur
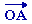 sur une droite est égale à sur une droite est égale à  cos
a
(a étant l’angle entre le vecteur
cos
a
(a étant l’angle entre le vecteur
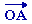 et la droite ( D )). et la droite ( D )).
3- Produit scalaire de deux
vecteurs :

Considérons deux vecteurs 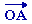 et
et  de même origine et faisant entre eux un angle q.
de même origine et faisant entre eux un angle q.
Le produit scalaire des deux vecteurs 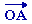 et
et  est défini par :
est défini par :
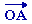 . .
 =
=   cos q
( 0 ≤ q
≤ p )
cos q
( 0 ≤ q
≤ p )
Les
propriétés :

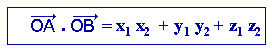
Le module d’un vecteur est défini par :
 =
= 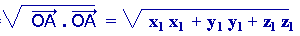
Remarque :
- Si 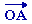 .
.  =
=  avec avec
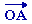 ≠
0 et
≠
0 et  ≠
0 alors
≠
0 alors 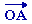 et
et  sont perpendiculaires.
sont perpendiculaires.
4- Produit vectoriel de deux vecteurs :

Considérons deux vecteurs 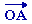 et
et  de même origine et faisant entre eux un angle q.
de même origine et faisant entre eux un angle q.
Le produit vectoriel des deux vecteurs 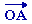 et
et  est le vecteur défini par :
est le vecteur défini par :
 =
=
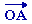
  de module
de module 
 sin q
( 0 ≤
q
≤ p
)
sin q
( 0 ≤
q
≤ p
)
Le vecteur  est perpendiculaire au plan contenant les deux vecteurs est perpendiculaire au plan contenant les deux vecteurs
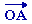 et
et  .
.
Le système ( 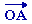 ,
,  ,
,  ) forme un trièdre direct. ) forme un trièdre direct.
Les propriétés :

5- Produit mixte de trois vecteurs :

Page Suivante
|