ÉLECTRICITÉ

(Suite)

3-7 Exemple : Étude des quadripôles (P=2 )
1) soit le quadripôle "Étoile" ou T suivant de matrice :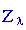
le sens des tensions et des courants est par convention comme dans le schéma :

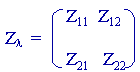
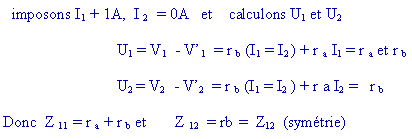
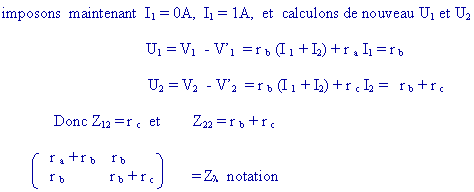
  2) soit le quadripôle " triangle" ou P suivant :

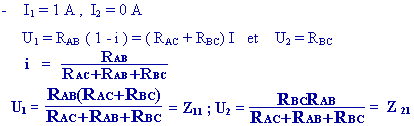
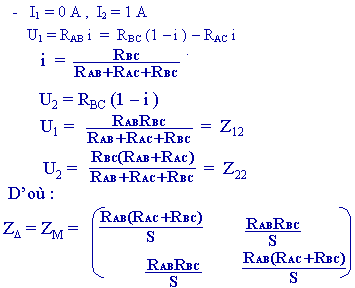
    3.8 Transfiguration Étoile   Triangle

Il est toujours possible de transfigurer une étoile à trois branches en un triangle et réciproquement.
En effet sachant les deux matrices des quadripôles Étoiles et triangle et comme deux multipôles sont électriquement équivalents si et seulement si leurs matrices sont identiques, on peut donc établir les formules de passage nécessaires.

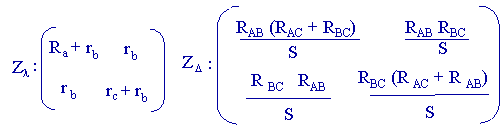
3.8.1 Transfiguration Triangle 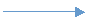     Étoile
On va chercher l'équivalent Étoile d'un triangle donné
Hypothèses : R_AB, R_AC et R_BC
Conclusion r_a = ? ; r_b = ? ; r_c : ?
De l'égalité des matrices Z_l= Z_D on déduit:

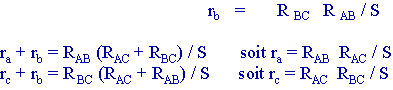
   Donc les résistances de l'étoile équivalente sont obtenues en divisant le produit des résistances adjacentes du triangle par la somme des résistances du triangle.

3.8.2 Transfiguration  Étoile 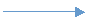   Triangle

   Cherchons maintenant l'équivalent triangle d'une étoile
Calculons : 

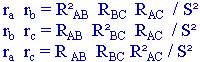
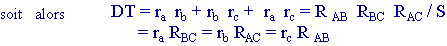
   Donc les résistances du triangle équivalent sont obtenues en divisant la somme des produits deux à deux des résistances des branches par la résistance de la branche opposée de l'étoile.

  Exemple :

   Bien entendu, ces formules de passage seront très utiles. Lorsqu'on a un groupement de résistance complexe (ni série, ni parallèle), avec des transfigurations triangle étoile, le groupement peut se ramener à un groupement simple (série, parallèle ou mixte).
Exemple :
Nous allons calculer la résistance équivalente vu entre A et B du circuit suivant : 

   Transfigurons le triangle D ACD en Étoile l ACD.

     Page Suivante