|
CHAPITRE
VI (Suite):
LES MULTIPÔLES PASSIFS
|
(Suite)
3.9 Théorème de
Thévenin
La théorie des circuits électriques nous montre qu'un réseau électrique actif quelconque, vu d'une paire de bornes est équivalent à un diplôme actif constitué d'une
fém E en série avec une impédance Z.
La relation U = E - ZI contient deux paramètres (E et Z) à déterminer.
· à vide (aucune impédance branchée entre les bornes A et B), le courant I parcourant l'accès est nul et U = E il suffit donc de mesurer U à vide.
· En court-circuit (résistance nulle branchée entre A et B), la tension U est nulle et
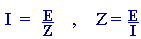

ÉNONCE
DU THÉORÈME
Tout réseau linéaire actif (c à d ne contenant que des éléments linéaires et des générateurs) ; vu d'une paire de bornes est équivalent à un dipôle actif constitué d'une f e m
Eth en série avec une impédance Zth (U = Eth -
Zth I)
Eth est la différence de potentiel à vide existant entre les bornes.
Z th est l'impédance équivalent du réseau, vue des bornes, toutes les sources de tensions étant
court-circuitées et tous les injecteurs de courant étant ouverts.
Exemple :
à vide U à vide = 10 i = 10 - 10 i
Þ
i = 0. 5 Þ
U à vide = 5 v =
Eth d'où circuit équivalent
3-10 Théorème de Norton
3.10.1 Introduction
Définissons tout d'abord ce que nous appelons injecteur de courant.
En fait c'est un dipôle actif ayant la propriété de fournir une intensité de courant indépendante de la valeur de la tension à ses bornes.
Pour ouvrir un injecteur de courant, il suffit de l'éliminer du circuit par contre court-circuiter une source de tension, c'est la remplacer par un fil (les résistances internes restent.
3.10.2 Énoncé du théorème de Norton
Tout réseau linéaire actif, vu d'une paire de borne est équivalent à un dipôle actif, constitué d'un injecteur de courant
Jn en parallèle avec une impédance
ZN.
Jn est l'impédance équivalente, vue des bornes, toutes les sources de tension étant
court-circuitées et tous les injecteurs de courant étant ouverts.
Exemple :
REMARQUE:
Zthévenin = ZNorton
3-11 Adaptation :
Nous avons vu au chapitre II (2-4) que lorsqu'on associe un dipôle actif (fem E, résistance interne r) avec une Résistance R, la puissance transférée du dipôle actif vers le dipôle passif sera maximale pour R = r cette puissance maximale est
:
Pm = E² / 4R.
Dans le cas d'un circuit quelconque, il y aura transfert maximum de puissance lorsqu'on branche à ses bornes une impédance Z égale à l'impédance de
thévenin de ce circuit
Zth.
La puissance transférée est Pm = E²th/4 Zth.
Exemple :
QUESTION :
Quelle est la puissance P consommée par la résistance externe R = 5
W,
Est-elle maximale ?
RÉPONSE :
Tout d'abord cherchons l'équivalent de thévenin du circuit
(en éliminant R = 5 W)
Page Suivante
|