ÉLECTRICITÉ

   3.4 Méthode des mailles
Comme nous l'avons précisé au paragraphe 1, chaque branche est constituée d'un dipôle et nous avons supposé tous les dipôles actifs.
Définitions :
1°) e_b : matrice unicolonne des f.é.m. de branches (B x 1). S'il n'y a pas de générateur pour la branche considérée, la composante correspondante de e_b sera 0.
2°) Z_b : matrice d'impédance de branche (B x B).

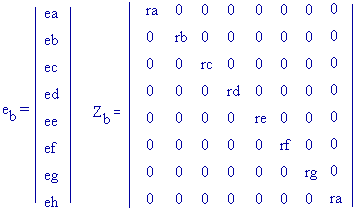
Pour toutes les branches nous aurons : u_b = e_b - z_b i_b
Exemple :

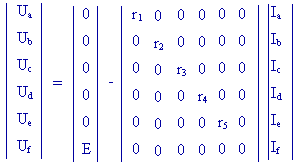
u_b = e_b - z_b i_b
Prémultiplions par t_C et remplaçons i_b = Ci_m ; tenant compte de la relation :  t_C U_b = 0

 t_C U_b = 0 =  t_C e_b -  t_C Z_b Ci_m soit : t_C e_b = t_C Z_b C i_m
Posons : t_C e_b = e_m
t_C matrice de M x B / e_m matrice unicolonne de M x 1 = matrice unicolonne des f.e. m de mailles / e_b matrice unicolonne de B x 1
t_C Z_b C = Z_m 
t_C matrice de B x B / t_C Z_b matrice de M x B
C matrice de B x M / Z_m = t_C Z_b C matrice de M x M

La relation t_C e_b  = t_C Z_b Ci_m s'écrira :     e_m = Z_m i_m 
Du réseau et du graphe on détermine : e_b ; Z_b ; C et de là on calcule
E_m =  t_C e_b  et Z_m = t_C Z_b C
E_m = Z_m i_m Constitue un système de M équations linéaires à M inconnues
Sa résolution conduit à la détermination 

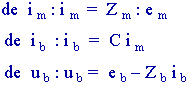
L'état électrique du réseau est ainsi complètement déterminé.
Marche à suivre
1°) On dessine le graphe du réseau donné, en fixant un sens conventionnel de circulation aux courants de branches.
2°) On choisit un arbre sur ce graphe
3°) On établit la matrice des mailles.
4°) On établit la matrice d'indépendances de branches et la matrice des f. e. m. de branches
5°) On calcule les matrices Z_m et e_m : Z_m = t_C Z_bC          e_m = t_C e_b
      Par résolution de e_m = Zi_m on détermine i_m et de là : i_b = Ci_m & u_b = e_b - Z_b i_b.

Exemple :

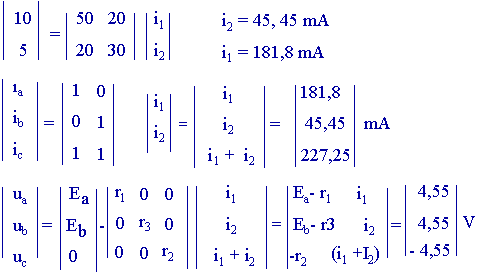
Puissance injectée dans un réseau
Rappel : t_(AB) = t_Bt_A
La puissance de chaque générateur, dans chaque branche est : gPj = -ej Ij
Pour tous les générateurs du réseau :

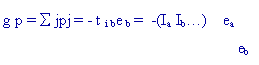
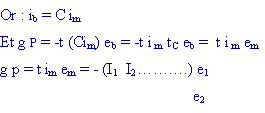
Dans l'exemple ci-dessus : gp = - i₁ Ea - i₂ E_b

Théorème de Tellegen :
Toutes les branches étant supposées actives, pour chaque branche la puissance sera : 

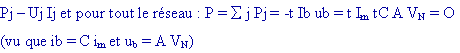
P = 0 signifie que le réseau n'échange aucune puissance électrique avec l'extérieur.
gP = -t i_m e_m puissance injectée dans le réseau par les sources de f.e.m.
pP puissance dissipée par tous les éléments passifs.
P = gP + pP = 0   ,    Pp = - gP = t i_m e_m 
Soit encore             t i _b e _b  + t i_b e_b  = 0
                                            ∑ Ij ej   =  ∑Rj Ij²

Toutes les branches     Toutes les branches
Puissance débitée             Effet joule total
Par les générateurs                                   

Page Suivante