|
CHAPITRE
IV (suite) :
TOPOLOGIE DES CIRCUITS
ÉLECTRIQUES
|
*1ère Relation de
Kirchhoff: loi des nœuds
Prenant comme convention de compter positivement les courants qui
arrivent aux nœuds et négativement ceux qui s'en écartent .

Les relations (II) ci-dessus peuvent s'écrire :
TA Ib = 0 où TA désigne la matrice
A transposée
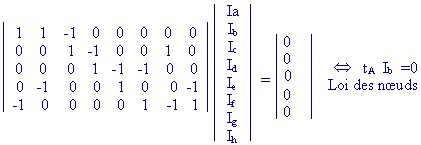
- La
matrice A est une matrice de B lignes et N colonnes où B désigne le
nombre de branches du réseau (ou du graphe) et N le nombre de nœuds.
- La matrice tA est une matrice de N lignes et B colonnes
- Chaque ligne de A contient des zéros, une fois + 1 et une fois -1 ;
la somme des colonnes de A aura pour résultat une colonne de zéros.
Ce qui indique que les 5 relations (II) sont linéairement dépendantes.
On peut démontrer
que si l'on supprime l'une quelconque de ces relations (équation du nœud
1 ou 2 ou 3 ou 4 ou 5). Les (N-1) relations restantes sont linéairement
indépendantes.
Cette relation (tA Ib = 0) permettra d'écrire
(N-1) courants en fonction des B - (N-1) = M courants restants.
Soit le graphe et l'arbre ci-dessous.
Arbre  A
= {gdeb} A
= {gdeb}

3.3
Deuxième matrice topologique : la matrice des mailles C
Reprenons le réseau adopté pour l'introduction de la matrice
d'incidence et choisissons un arbre et dès lors un co-arbre.
Formons dans le réseau considéré à partir de chacun des maillons
et en n'empruntant que des branches de l'arbre, un ensemble de
mailles, conformément à la définition de ces dernières.
Arbre  A
= { g d e b } A
= { g d e b }
Orientons la maille dans le sens du maillon définissant la maille

La matrice
des mailles C définit les appartenances entre branches et mailles,
elle est uni modulaire et d'ordre B x M.
Chaque ligne de C spécifie les mailles passant par une branche donnée
: La valeur + 1 signifie que le sens de la maille coïncide avec le
sens de la branche, la valeur -1 marque l'opposition de sens, le
nombre 0 exclut le passage de la maille par la branche considérée.
Chaque colonne de C spécifie, pour une maille donnée, les branches
par lesquelles passe cette maille, avec la même interprétation des
sens.
Si l'on forme la matrice tC (transposée de la matrice C) ;
ce sont évidemment les lignes de cette dernière qui fournissent les
mêmes informations.
*2ème relation de
Kirchhoff : Loi des mailles
La dernière remarque précédente permet d'exprimer directement la
deuxième loi de Kirchhoff pour l'ensemble des mailles d'un graphe.
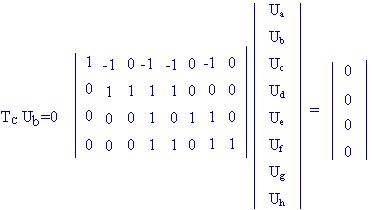
Relation
entre courant de branches Ib et courants de maillons Im
La
relation (IV) du paragraphe 2. Fait apparaître une matrice qui n'est
d'autre que la matrice des mailles C.
Soit ib = C im avec im matrice
unicolonne des courants de mailles (= courants dans les maillons)

m
est de dimension : (M x 1)
La
relation : ib = C im donne une autre
interprétation physique de la matrice C.
Une
maille, parcours fermé, est le siège d’un courant (partie « commune »
à toutes les branches constituant la maille), soit 1 siège d’un
courant I1.
Comme
d’autre part chaque maillon définit une maille, et n’appartient
qu’à une seule maille, il ne sera traversé que par le courant de
maille I1, a l’exclusion = Ia de même :
I2 = Ic ; I3 = If ; I4
= Ih.
Par
contre les branches de l’arbre peuvent être traversées par des
courants de mailles différents (parce que appartenant simultanément
à des mailles différentes). L’appartenance d’une branche à une
ou plusieurs mailles est donnée par la ligne correspondante de la
matrice C, sens compris.
Exemple
:
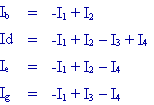
Remarque
:
1) Le système de M équation
: tC Ub = 0 constitue un système de M équations
linéairement indépendants. Pour s'en convaincre il suffit de
permuter les tensions de branches (et les colonnes correspondantes de
tC pour faire apparaître les maillons en première
position.

2)
Les relations ib = C im et tC Ub
= 0 permettent de résoudre complètement le système.
Page Suivante
|