|
Éléments de Mathématiques
|
Plan
1. Développements
en série
2. Calcul
des expressions indéterminées
3. Calcul
différentiel
4. Différentielles
d'ordre supérieur
5. Différentielles
des fonctions de plusieurs variables indépendantes
6. Calcul
intégral
7. Eléments
d'analyse vectorielle
Rappel : soit une fonction  ;
on appelle dérivée de la
quantité égale à  .
Prérequis : calcul de dérivées
1. Développements en série
Soit une fonction définie pour des intervalles de variation de x où elle ne
devient pas infinie et où les dérivées existent.
Théorème des accroissements finis : Pour une telle
fonction, il existe toujours une abscisse c comprise entre a
et b telle que :
Formule de Mac-Laurin
Formule de Taylor
Application aux développements en série
On montre que :
 
 
Remarque : Les séries obtenues sont soumises à
des conditions de convergence que nous ne développons pas ici. On
montre que les trois premières séries données sont valables pour
tout x, la quatrième pour -1 < x < 1.
Utilité des développements en série pour les applications
numériques
2. Calcul des expressions indéterminées
Premier moyen Il suffit de développer le numérateur et
le dénominateur en série de Maclaurin et de simplifier.
Deuxième moyen. Règle de L’Hopital
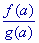 se présente
sous la forme  ,
alors
 démonstration
à partir du théorème des accroissements finis.
Par exemple, 
3. Calcul différentiel
Le calcul différentiel et intégral a été inventé par Newton
et Leibnitz à la fin du XVII ème
siècle à la suite d’un grand nombre de travaux mathématiques
ayant abouti à l’étude des dérivées, des tangentes aux courbes
et des infiniment petits. Ce calcul a été ensuite mis au
point par différents mathématiciens (Euler, Laplace, Cauchy, ...)
qui lui ont donné sa forme actuelle.
On faisait déjà de l’algèbre avant Jésus-Christ et le célèbre
Archimède savait résoudre certaines équations du 2
ème degré ; on doit donc convenir que, du moment
qu’il a fallu attendre l’arrivée de Leibnitz et de Newton, il y
a trois cents ans seulement, c’est que ce calcul est subtil et
transcendant, et d’un niveau supérieur aux mathématiques élémentaires.
Il exige une certaine tournure d’esprit.
Les infiniment petits. Un infiniment petit est une quantité
variable qui tend vers 0.
Exemples,
 quand x
tend vers 0 tend aussi vers 0, c’est donc un infiniment petit
 quand x
tend vers 0 tend aussi vers 0, c’est donc un infiniment petit.
On dira que  sont
des infiniment petits équivalents si la limite du rapport  tend
vers 1, quand tendent
vers 0.
On montrera, par exemple, que l’infiniment petit  est
équivalent à l’infiniment petit x ou que l’infiniment
petit  est équivalent
à  .
Les différentielles
La petitesse d’une grandeur est relative. Une minute comparée
à une heure est très petite, mais une minute comparée à une
seconde est très grande.
Dans le calcul différentiel, on appelle dx une très
petite variation donnée à la variable x en plus ou en
moins. On peut la prendre aussi petite que l’on veut, mais elle
est fixe et il n’est pas question de la faire tendre vers 0
comme un Dx.
dx a un caractère algébrique.
En effet, soit par exemple, 
 
Appliquons la formule de Taylor
On appelle différentielle de y ou de f(x)
la quantité dy = y’dx ou df = f’(x)dx
dy a un caractère algébrique.
Calcul des différentielles
Application de la définition 
Différentielles d’une somme, d’un produit, d’un
quotient
Soient u et v des fonctions de x.
Différentielles des fonctions de fonctions
Soit y = f(u) avec u = u(x)
Quelques applications simples des différentielles
- On chauffe un disque en métal et son rayon croît à la
vitesse de 1 mm par seconde. Calculer la vitesse à laquelle croît
la surface S du disque si le rayon R = 10 cm ?
- Différentielles des fonctions paramétriques
- Différentielle logarithmique
Exemple : 
4. Différentielles d’ordre supérieur
Nous avons vu que la différentielle de y = f(x) est dy
= y’ dx où dx est aussi petit que l’on veut mais fixé.
Nous cherchons la différentielle de dy c’est à dire d(dy)
que nous noterons  (prononciation
" d deux y ").
Par définition,  =
(dérivée de dy).dx (dérivée de dy) = (y’dx)’
= y’’dx
On aurait de même 
5. Différentielles des fonctions
de plusieurs variables indépendantes
En Physique, nous avons souvent à étudier les fonctions de
plusieurs variables indépendantes. Nous nous limiterons à deux notées
x et y mais les résultats sont facilement généralisables.
Soit une fonction f(x, y), nous appellerons différentielle
de f (notation df) la quantité 
est la dérivée de f par rapport à x, la variable y
étant considérée comme une constante dans la dérivation
(prononciation d rond f sur d rond x).
La différentielle apparaît comme la somme des différentielles
partielles.
Un grand nombre de mathématiciens prennent a priori cette formule
comme définition de la différentielle et ne la démontrent pas.
Que les esprits ... rigoureux sachent qu’elle se démontre.
L’application de cette formule aux calculs d’erreur est
chose importante pour un expérimentateur.
Théorème : soit une fonction de deux variables f(x,
y), on a toujours 
Autrement dit : pour la dérivée seconde croisée l’ordre de dérivation
importe peu ; que l’on commence par x et que l’on
continue par y, ou que l’on commence par y et que
l’on continue par x, le résultat est le même.
Remarque importante sur la différentielle
d’une fonction
Soit une forme différentielle A(x, y) dx + B(x, y) dy
différentielle d’une fonction f(x, y) c’est à dire
telle que df = A(x, y) dx + B(x, y) dy, alors par définition
de la différentielle d’une fonction f(x, y) nous avons,
Le théorème sur les dérivées croisées nous permet d’établir
la relation très importante de Cauchy,
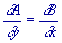
La conséquence de cette relation est simple.
Soit une forme différentielle A(x, y) dx + B(x, y) dy,
- les coefficients A(x, y) et B(x, y) obéissent
à la relation ci-dessus, alors il existe une fonction f(x,
y) telle que df = A(x, y) dx + B(x, y) dy.
On dit, ce qui est équivalent, que la forme différentielle A(x,
y) dx + B(x, y) dy est une différentielle totale exacte.
- les coefficients A(x, y) et B(x, y) n’obéissent
pas à la relation ci-dessus, alors la fonction f(x,y)
n’existe pas.
La forme différentielle A(x, y) dx + B(x, y) dy n’est
pas une différentielle totale exacte.
En Physique (plus particulièrement en Thermodynamique),
- nous avons des formes différentielles qui sont des différentielles
totales exactes, nous les notons df et nous sommes
amenés à calculer la fonction f(x, y).
C'est le cas de ce que nous appelons les fonctions d’état
(la fonction U (énergie interne), ou la fonction H
(enthalpie) ou la fonction S (entropie) ou ...).
- nous avons des formes différentielles qui ne sont pas des
différentielles totales exactes, nous les notons dg
ce qui veut dire que la fonction g(x, y) n’existe pas.
C'est le cas de dW et dQ
qui sont des quantités, respectivement de travail et de
chaleur, élémentaires (aussi petites que l’on veut) échangées.
Nous devons comprendre d comme l’opérateur mathématique
différentiel et dg
comme une quantité élémentaire.
Exemples
 
Il existe une fonction f(x, y) telle que 
que nous apprendrons à calculer.
 
Il n’existe pas de fonction g(x, y) et la notation sera
6. Calcul intégral
Le calcul intégral est l’opération inverse du calcul différentiel
à savoir,
- trouver une fonction f(x) dont la dérivée
- en notation différentielle, ceci peut se dire, trouver une
fonction f(x) dont la différentielle est df = f’(x)
dx.
La notation pour cette opération est la suivante :
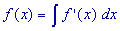(prononciation somme de ou primitive de f’(x) dx)
Prérequis : Calcul de primitives (intégrales indéfinies)
Calcul des fonctions f(x, y) dont on connaît la différentielle
 . Cette
primitive est faite en traitant y comme une constante si bien
que la constante d’intégration peut être fonction de y.
on obtient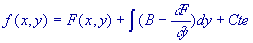 
où il faut bien comprendre que F(x, y) est une primitive par
rapport à x de A(x, y) et que la variable x
s’est éliminée dans  .
- Nous prenons, à titre d’exemple,
Le lecteur, pour bien comprendre la méthode, aura intérêt
à recommencer le calcul à partir de  .
Remarque :
Très souvent, en Thermodynamique, A(x, y) ne sera fonction
que de x et B(x, y) que de y. Alors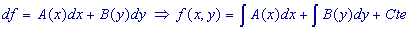 
Le calcul se ramène à celui de deux primitives ordinaires.
Calcul des intégrales curvilignes
On appelle intégrale curviligne l’expression suivante,
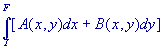 d’un point I à
un point F suivant une courbe d’équation h(x, y) = 0.
(En Thermodynamique, on dit d’un état initial I à un état
final F suivant une transformation)
Le calcul direct se fait en remplaçant y et dy en
fonction de x et de dx à partir de h(x, y) = 0
dans l’intégrale curviligne et le calcul devient celui d’une
intégrale simple.
- Le cas particulier où
mérite d’être étudié. c’est
à dire que le résultat ne dépend pas de la courbe, il ne dépend
que des points I et F (en Thermodynamique, nous dirons que le résultat
ne dépend pas de la transformation et qu’il ne dépend que
des états initial et final).
Dans ce cas, nous disposons de deux méthodes pour calculer
l’intégrale curviligne.
7. Eléments
d'analyse vectorielle
Opérateur gradient
Soit une fonction f(x, y, z) c’est à dire une fonction
des trois variables cartésiennes x, y et z.
Par définition 
où  sont les
vecteurs unitaires de la base cartésienne habituelle (prononciation
: gradient de la fonction f au point M(x, y, z)).
Propriété
Soient  le
vecteur position et 
Opérateur divergence
Soit un vecteur 
où les composantes sont des fonctions des variables x, y
et z.
Par définition 
Opérateur Laplacien
Soit une fonction f(x, y, z) c’est à dire une fonction
de trois variables indépendantes x, y et z.
Par définition 
Propriété : 
| 
