abcsite.free.fr
![]()
Chimie Organique
|
|
6. Techniques d’analyses spectroscopiques
| Dans ce chapitre | |
| 6.1. | Spectroscopie de résonance magnétique nucléaire |
| 6.2. | Spectroscopie U.V.-Visible et systèmes p délocalisés |
| 6.3. | Spectroscopie infrarouge |
| 6.4. | Spectrométrie de masse |
Parmi les méthodes d’analyse courantes non destructrices, citons:
Point de fusion Point d’ébullition Solubilité
Acidité Indice de réfraction Pouvoir rotatoire
Toutefois, ces méthodes ne sont pas suffisantes pour déterminer la structure moléculaire.
Les méthodes spectroscopiques (spectrum, latin, apparence, apparition, faisant allusion de lignes caractéristiques obtenues lors de la prise de "spectres") sont souvent utilisées pour analyser les molécules organiques et identifier correctement les groupements fonctionnels présents, principalement parce que ce sont des techniques d’analyse non destructrices.
Tout d’abord, passons rapidement en revue les différentes parties du spectre électromagnétique. La Figure 10.2 (Vollhardt p.326-327) nous donne une bonne idée de l’étendue de ce spectre et des diverses régions utiles. Dans ce cours, nous nous intéresserons plus particulièrement aux domaines des:
ondes radios 0.1 à 1 m, nous donnerons des informations quant au nombre, à la nature et à l’environnement des atomes d’hydrogène et de carbone
infrarouge 2 à 15
m (1m=10-6 m), nous donnerons des informations sur la nature des groupes fonctionnels présentsvisible 400 à 700 nm (1nm=10-9 m), nous donnerons des informations sur les diverses transitions électroniques et la conjugaison des molécules
ultraviolet 200 à 400 nm, nous donnerons des informations sur les diverses transitions électroniques et la conjugaison des molécules
| L’étudiant est prié de relire les pages 324 à 327 si ces notions de spectres électromagnétiques sont floues, car ce n’est pas le but du cours de faire une étude exhaustive de la spectroscopie. |
6.1. Spectroscopie de résonance magnétique nucléaire (Vollhardt 10 et Pavia 3 et 4)
La RMN fait appel au comportement des noyaux atomiques lorsque ceux-ci sont soumis à un champ magnétique. On peut considérer chaque noyau comme une toupie qui présente un spin nucléaire. Étant donné que les noyaux sont chargés positivement, ce mouvement de spin nucléaire engendre un moment magnétique. Ainsi, ce noyau se comportera-t-il comme un minuscule barreau aimanté.
Lorsque ce barreau aimanté sera soumis à un champ magnétique externe, Ho, il aura la possibilité de s’orienter parallèlement ou anti-parallèlement à ce même champ, tout comme l’aimant d’une boussole. Il est évident que l’orientation parallèle,
a, sera énergétiquement plus favorable que l’orientation anti-parallèle, b (Figure 10.4, Vollhardt p.328), mais à la température ambiante une répartition statistique existe entre les deux états de différente énergie.C’est précisément cette différence d’énergie qui est mise à profit ici. L’irradiation de l’échantillon produira une transition de l’état
a vers l’état b (Figure 10.5, Vollhardt p.329). De plus, étant donné que nous assistons à un phénomène de résonance, l’excitation et la relaxation sont continuels, contrairement aux autres types de spectroscopie.Évidemment, la différence d’énergie, D E, entre les deux états dépendra directement de la force du champ magnétique H
o selon: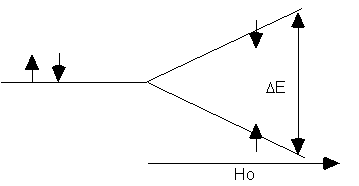
La fréquence d’absorption est égale à:
n
= k Ho, ou nous avonsh
est la constante de Planck, et g est le rapport magnétogyrique, une constante pour un noyau donné. De plus, la valeur de k est proportionnelle à son environnement chimique.Quelle est la valeur de D E? Les aimants commerciaux possèdent des champs magnétiques de l’ordre de 14 à 150 kilogauss. Les valeurs de fréquence correspondantes pour observer la résonance varient entre 60 et 600 MHz et elles se situent dans le domaine des ondes radio. Ces valeurs indiques un D E de l’ordre de 10-6 à 10-5 kcal•mol-1. C’est ce qui explique qu’à la température de la pièce il y ait une répartition presque égale des deux populations
a et b.Les noyaux qui peuvent montrer ce phénomène de résonance magnétique nucléaire sont relativement peu nombreux. En effet, ils doivent répondre à certaines conditions. Ils doivent posséder une masse atomique impaire ou un numéro atomique impair ou les deux. Chaque noyau est caractérisé par un nombre quantique de spin, I. Le nombre d’orientation possibles dans un champ magnétique est donné par 2 I + 1. Le tableau suivant donne les nombres quantiques de spin pour plusieurs noyaux.
|
Élément |
|
|
|
|
|
|
|
|
|
|
||
|
Nombres quantiques de spin |
½ |
1 |
0 |
½ |
1 |
0 |
2 ½ |
½ |
½ |
1 ½ |
||
|
Nombre d’orientations possibles |
2 |
3 |
1 |
2 |
3 |
1 |
6 |
2 |
2 |
4 |
||
Le Tableau 10.1 (Vollhardt p.330) montre quelles sont les abondances relatives des noyaux importants et leur activité RMN. On peut voir que seuls ceux qui possèdent un nombre quantique de spin non nul sont actifs en RMN.
Les noyaux qui présentent 2 orientations possibles sont les plus utilisés: 1H, 13C, 19F et 31P.
Comme le montre la Figure 10.6 (Vollhardtp.330) le spectre du CHDFCl pourrait donner le spectre présenté. On peut voir que le balayage en fréquence s’étend sur une large fenêtre. Si on double la force de Ho, on doublera les fréquences observées. Cela est mis a profit pour augmenter la résolution tel que montré à la Figure 10.7 (Vollhardt p.331) et séparer les pics autrement indiscernables.
Ceci dit, comment est fait un spectromètre de RMN? Nous possédons à l’UQTR un appareil de 60 MHz. Présentement, des appareils fonctionnant à des forces de champ énormes correspondant à des fréquences de 500 MHz.
Dans ce type de spectrométrie, on dissous l’échantillon dans un solvant approprié. On met la solution dans un tube que l’on introduit dans l’électroaimant. On fait osciller l’intensité du champ magnétique à radiofréquence constante et on détecte l’absorption des diverses radiofréquences.
6.1.1. Le déplacement chimique du proton (Vollhardt 10.4, Pavia 3.5 et 3.8)
La Figure 10.8 (Vollhardt p.333) montre le spectre RMN du chloro(méthoxy)méthane. On peut voir qu’il y a 2 signaux. Pourquoi?
La position du pic est contrôlée par le blindage ou le déblindage électronique du noyau, entre autres termes, son environnement chimique.
Le champ Ho induit un courant électronique au niveau des électrons liants situés autour d’un noyau d’hydrogène, qui à son tour génère un champ magnétique local s’opposant à Ho (loi de Lenz) (Figure 10.9, Vollhardt p.334). Cet effet de blindage se répercute sur la position relative du spectre RMN. En effet, le noyau subira un champ magnétique local:
Ho - hlocal
qui impliquera une diminution de la fréquence nécessaire pour provoquer la résonance (Figure 10.10, Vollhardt p.334). De la façon dont on enregistre les spectres, un déplacement vers les champs plus forts signifie que le signal (pic) apparaît plus loin à droite.
De la même façon, si le champ magnétique local augmente le champ externe H
o (ce qui est fréquent avec les atomes fortement électronégatifs), nous observerons un déplacement vers les champs plus faibles (gauche). On dit alors que les protons subissent un déblindage. Ainsi, les hydrogènes de CH3OH sont plus déblindés que ceux de CH3I, parce que l’électronégativité de O est plus grande que celle de I.Expérimentalement, plutôt que de rapporter la fréquence exacte de résonance (difficile sur le plan technique), on ajoute un standard interne par rapport auquel les pics sont mesurés. En ce qui concerne la RMN-1H, ce standard est le tétraméthylsilane, Si(CH3)4, TMS (Eb=26.5°C). Ce composé est utilisé parce que les 12 hydrogènes équivalents sont particulièrement bien blindés par rapport à ceux de la plupart des composés organiques. De plus, la plupart des solutions commerciales de solvants de qualité RMN, deutérés ou non comme le CCl4, sont disponibles avec environ 1% de TMS.
On peut alors mesurer le déplacement en fréquences par rapport au pic du TMS. cependant, un problème demeure. En effet, l’intensité du champ et la fréquence de résonance sont intimement liés. Ainsi, les spectres seront différents d’un spectromètre à l’autre. Pour éviter cette complication, et aux fins de comparaison, on standardise la fréquence mesurée pour la rendre indépendante du champ. Nous obtenons alors une mesure appelée déplacement chimique définie selon:
d
=Le déplacement chimique est exprimé en parties par million (ppm), des unités qui dans le cas de l’hydrogène présentent 3 chiffres significatifs. Ainsi, par définition:
d
(Si(CH3)4) = 0.00 (Figure 10.11, Vollhardt p.335)Ces déplacements en ppm sont mesurés par rapport au signal du TMS (charte simplifiée page suivante).
Le Tableau 10.2 (Vollhardt p.337) montre les déplacements chimiques des protons soumis à divers environnement chimiques. Il est important de noter les valeurs généralement observées pour les groupements fonctionnels que nous avons vu: alcanes, halogénoalcanes, alcools, éthers et amines. On peut spécialement voir que dans le cas des alcools et des amines, les valeurs de ces déplacements chimiques est extrêmement variable en fonction de la concentration. Ils dépendent surtout des liaisons hydrogène. Ainsi
d diminue en fonction de la dilution.Le Tableau 10.3 (Vollhardt p.337) montre aussi à quel point l’électronégativité d’un hétéroatome influence le déplacement chimique en le déplaçant vers les bas champs (déblindage). De plus, cet effet est cumulatif, mais diminue rapidement à mesure que le nombre de liaisons interposées augmente.
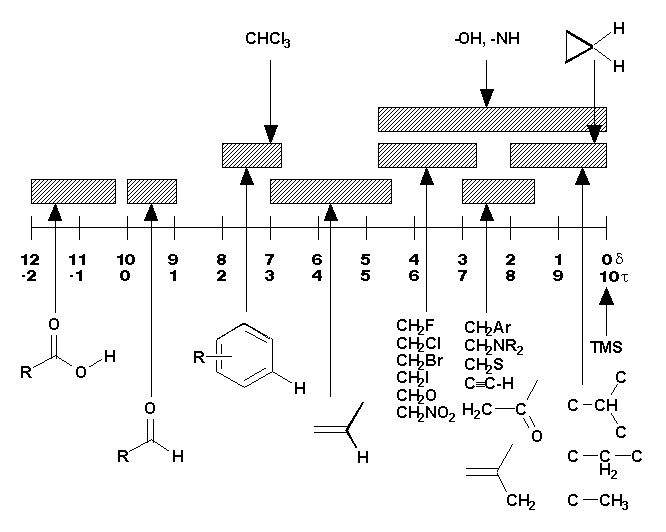
Charte simplifiée d'attribution en RMN-1H
| 0-2 ppm | 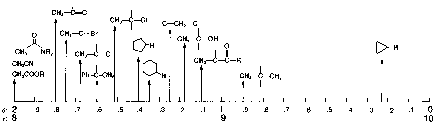 |
.gif (49 kB) | Photoshop (107 kB) |
| 2-4 ppm | 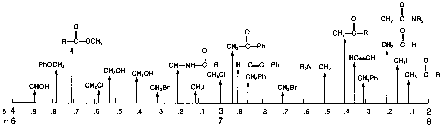 |
.gif (53 kB) | Photoshop (117 kB) |
| 4-6 ppm | 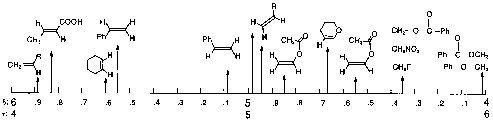 |
.gif (53 kB) | Photoshop (119 kB) |
| 6-8 ppm |  |
.gif (68 kB) | Photoshop (157 kB) |
| 8-10 ppm | 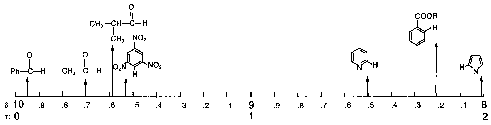 |
.gif (39 kB) | Photoshop (91 kB) |
| 10-12 ppm | 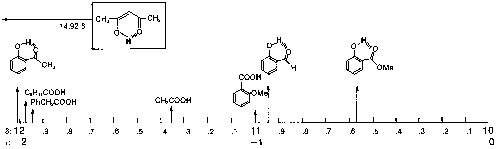 |
.gif (50 kB) | Photoshop (115 kB) |
6.1.2. Hydrogènes équivalents (Vollhardt 10.5, Pavia 3.7)
Tels que présentés dans les exemples des Figures 10.8 et 10.11, nous avons vu que 2 ou plus de 2 hydrogènes occupant des positions qui sont chimiquement équivalentes donnent lieu à seulement une absorption en RMN. On peut dire que des protons chimiquement équivalents présentent le même déplacement chimique. Toutefois, l’inverse n’est pas nécessairement vrai, les protons présentant des même déplacement chimiques ne sont pas nécessairement chimiquement équivalents.
Cette équivalence peut être établie par la symétrie des molécules. Si deux protons liés sur un atome sont images spéculaires l’un de l’autre, ou si une rotation les interconvertis, alors ils sont chimiquement équivalents (Figure 10.12, Vollhardt p.338).
Ce concept d’équivalence est démontré à la Figure 10.13 (Vollhardt p.338) ou l’on montre divers types de protons chimiquement équivalents.
Maintenant, qu’en est-il du spectre RMN du cyclohexane. À température de la pièce, son spectre ne montre qu’un seul pic. Or, nous savons qu’il contient 2 types différents de protons, axiaux et équatoriaux. Il en est de même avec le chloroéthane qui présente des types de protons différents selon la projection de Newman utilisée (Figure 10.14, Vollhardt p.339). Cela est possible parce que les rotations et interconversions des formes chaises sont plus rapides que l’échelle de temps nécessaire à la prise d’un signal RMN.
Au fur et à mesure que l’on abaisse la température, la vitesse d’interconversion chaise-chaise diminue et de moins en moins de molécules possèdent l’énergie suffisante pour vaincre la barrière d’énergie. À -100°C, le spectre RMN du cyclohexane présente deux signaux correspondant l’un aux hydrogènes axiaux, l’autre aux hydrogènes équatoriaux. Par augmentation de la température, les deux signaux se rapprochent graduellement pour se confondre à -66.7°C (température de coalescence). À titre de comparaison, le point de fusion du cyclohexane est de 6.6°C. Ainsi, les hydrogènes Hb du chloroéthane s’équivalent par rotation rapide.
En ce qui concerne les Ha du chloroéthane, on peut voir à la Figure 10.14 sont des images miroirs l’un de l’autre car il existe un plan de symétrie dans la molécule. La substitution de l’un des deux par un substituant fournit une paire d’énantiomères. On dit qu’ils sont énantiotopiques. Par contre, ce n’est pas le cas avec le 1-chloro-2-fluoropropane. Ici, il n’existe aucun plan ni centre de symétrie. La substitution de l’un des deux par un substituant fournit un nouveau centre asymétrique, avec pour résultat la formation de diastéréoisomères. Ces noyaux sont donc qualifiés de diastéréotopiques. Étant chimiquement non équivalents, ils donneront deux signaux différents. Cette observation s’applique à tous les composés chiraux contenant un groupement méthylène portant 2 (pas plus) substituants identiques.
Une molécule ne doit pas nécessairement être chirale pour posséder des noyaux diastéréotopiques. Le même phénomène est observé dans le cas de cyclohexanes monosubstitués tel le bromocyclohexane. Ici, la conformation du brome équatorial est favorisée, parce qu’il est très gros. Ainsi, les hydrogènes Ha et He sont-ils magnétiquement différents et diastéréotopiques.
Malgré cette différence, ils ne fournissent qu’un doublet à
d = 4.06 ppm lorsque le spectre est enregistré à 22°C. Cependant, à -84°C, deux multiplets distincts sont observés: l’un à d = 3.87 ppm (Ha) pour la conformation du brome équatorial et l’autre à d = 4.59 ppm (Ha) pour la conformation du brome axial. Les surfaces des pics révèlent des fractions molaires de 70 % et 30 % respectivement.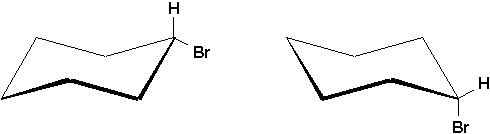
Lorsque cet effet d’interconversion est empêché par un énorme groupement, comme un tert-butyle qui "gèle" la conformation dans lesquelles il est en position équatoriale, les hydrogènes diastéréotopiques présentent des signaux différents.
Les différences de déplacement chimiques des groupes diastéréotopiques sont souvent minimes et donnent souvent lieu à une seule absorption comme s’ils étaient équivalents, ce qui explique souvent les pics évasés observés à basse résolution.
6.1.3. L’intégration des pics (Vollhardt 10.6)
Une des caractéristique intéressante des spectres RMN est que l’intensité relative d’un signal correspond à l’abondance relative du noyau qui en est la cause. En mesurant l’aire sous la courbe des signaux (ou l’intégrale de la fonction) et en la comparant aux autres signaux, il est possible d’estimer quantitativement les rapports des noyaux.
Un exemple est montré à la Figure 10.15 (Vollhardt p.342). Les rapports de hauteur obtenus indiquent alors les rapports du nombre de protons. Ceci permet donc de différencier rapidement plusieurs isomères.
Prenons par exemple les 2 isomères suivants (valeurs de
d indiquées):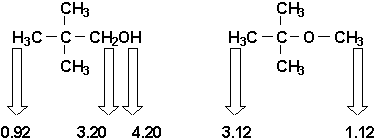
Les rapports d’intégration nous donneront 1:2:9 pour le 2,2-diméthylpropanol et 1:3 pour le 2-méthoxy-2-méthylpropane. Il devient donc aisé de pouvoir déterminer l’identité de ces 2 isomères.
6.1.4. Couplage spin-spin (Vollhardt 10.7, Pavia 3.11-2)
Jusqu’à maintenant, nous avons vu les spectres RMN de composés qui présentent un point commun: les hydrogènes non équivalents sont séparés par au moins un noyau qui ne porte pas d’hydrogène.
Lorsque des noyaux voisins non équivalents sont présents
, il se produit une complication: le couplage spin-spin. Il est résultera des multiplets au lieu de pics simples. Un tel exemple est présenté à la Figure 10.16 (Vollhardt p.344).Cette caractéristique importante nous aide à établir complètement la structure d’un composé inconnu.
La Figure 10.17 (Vollhardt p.345) montre l’explication de ce phénomène. L’effet du spin de Ha se transmet à Hb par l’intermédiaire des électrons des liaisons. En effet, le proton Hb peut posséder 2 orientations ( ou ¯ ). Il en résultera un champ local amplifiant ou diminuant extérieur, Ho. Ainsi, le champ local subit par Ha sera-t-il Ho±hlocal. Le pic sera donc scindé en un doublet. De plus, l’intégration de chacun de ces pics montrera-t-il la contribution de 0.5 hydrogène. La surface totale de ce doublet sera de 1.
Le signal provenant de Hb sera influencé de la même façon par Ha. On observera que la distance (en Hz) entre les pics individuels de chaque doublet est la même. On désigne cette distance par le terme constante de couplage, J. Il est à noter que cette constante de couplage est indépendante du champ extérieur. Ce couplage ne s’observe qu’entre des protons géminés (geminus, latin, jumeau) ou vicinaux (vicinus, latin, voisin) (Figure à gauche de la p.346 dans Vollhardt). Jab varie entre 0 et 18 Hz pour les hydrogènes géminés et entre 6 et 8 Hz pour les hydrogènes vicinaux. Il est pour ainsi dire nul si les hydrogènes sont séparés de 3 liaisons ou plus. De plus, les noyaux équivalents quant au déplacement chimique ne présentent pas de couplage spin-spin.
Lorsqu’un Ha est sous l’influence de 2 Hb (identiques entre eux):
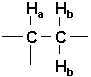
ceux-ci peuvent avoir les orientations suivantes:
, ¯ , ¯ , ¯ ¯On voit que les deux conformations du milieu sont équivalentes et ne créeront pas de modification de Ho. Ha apparaîtra donc comme un triplet dont le pic central est le double de la surface des deux autres pics. Les rapports de pics seront 1:2:1. Le pic central ne subira pas de modification du déplacement chimique (Figure 10.19, Vollhardt p.347).
Lorsqu’un Ha est sous l’influence de 3 Hb (identiques entre eux):

ceux-ci peuvent avoir les orientations suivantes:
, ¯ , ¯ , ¯ , ¯ ¯ , ¯ ¯ , ¯ ¯ , ¯ ¯ ¯On voit que les conformations 2-3-4 sont équivalentes et inverses de 5-6-7. Toutes vont créer une modification de Ho. Ha apparaîtra donc comme un quadruplet centré entre les deux pics du milieu. Les rapports de pics seront 1:3:3:1. (Figure 10.20, Vollhardt p.347).
Il existe une règle qui simplifie ces résultats, c’est celle de la fragmentation spin-spin simplifiée, ou la règle N + 1.
Lorsqu’un hydrogène possède N hydrogènes voisins chimiquement différents de lui même mais identiques entre eux, il en résultera un multiplet possédant N + 1 pics
nombre de pics = nombre de voisins +1
Il est aussi intéressant de noter que les rapports d’intégration des pics individuels suit la règle du triangle de Pascal. Le Tableau 10.4 (Vollhardt p.348) et les Figures 10.21, et 10.22 et 10.26 (Vollhardt p.348-9) montrent des exemples appropriés. De plus, il est important de noter que la Figures 10.21 montre l’exemple caractéristique d’un groupement éthyle, alors que la Figure 10.22 montre les problèmes associés aux pics fragmentés. Le Tableau 10.5 (Vollhardt p.351) montre des exemples de couplages spin-spin les plus fréquemment observés avec les groupes alkyle courants.
6.1.5. Couplage spin-spin: complications (Vollhardt 10.8)
Il existe des cas à problèmes, notamment lorsque les hydrogènes possèdent des
d semblables ou lorsque les constantes de couplages des voisins sont trop différentes. De plus, il est fréquent de voir apparaître un hydrogène hydroxylique sous la forme d’un singulet, et ce même s’il possède des hydrogènes vicinaux (Figure 10.15a). Ce pic est aussi sujet à un déplacement en fonction de la concentration.Ainsi, la répartition selon le triangle de Pascal et la règle N + 1 n’est possible que dans les cas ou D
d >> J. Il en résulte ce que l’on appelle un spectre du premier ordre.Dans une bonne majorité des cas, on peur voir que les motifs des pics sont biaisé. Prenons par exemple la Figure 10.21. Dans de pareils cas, on voit que les pics d’un multiplet sont biaisé dans la direction de la fréquence de résonance de noyaux responsable de la scission. Prenons le triplet à 1.6 ppm. Le pic de gauche est plus haut que celui de droite. Les 2 hydrogènes responsables se trouvent à 3.2 ppm (à gauche). Regardons le quadruplet, les 2 pics de droite sont plus haut que leur contrepartie de gauche. Ici, les 3 hydrogènes responsables sont à droite. Dans plusieurs cas, cela facilite l’interprétation des spectres.
Un autre exemple frappant de spectre qui n’est pas du premier ordre est présenté à la Figures 10.23 (Vollhardt p.352). On peut voir que même les alcanes simples présentent des complications, parce que les valeurs de
d de chacun des hydrogènes sont similaires, mais pas identiques.Toutefois, dans certains cas, comme pour le 2-chloro-1-(2-chloroéthoxy)-éthane, ClCH2CH2OCH2CH2Cl, les effets du blindage du chlore et de l’oxygène sont similaires et un spectres complexe symétrique complexe de 32 pics en résulte (Figure 10.24a, Vollhardt p.353). Ici, D
d » J. Comme d est proportionnel à l’intensité du champ externe, mais que J est indépendante de ce même champ, il est possible d’enregistrer le spectre sous un champ très intense pour obtenir D d >> J et ainsi résoudre le spectre en un profil de premier ordre (Figure 10.24b, Vollhardt p.353).Il se peut aussi que les voisins ne soient pas équivalents et qu’il en résulte un patron complexe, mais qui est quand même du premier ordre. Le spectre du 1-bromopropane de la Figure 10.27 (Vollhardt p.355) en est un exemple. En effet, la règle N + 1 n’est valable que dans le cas des scissions provoquées par des voisin magnétiquement identiques. Dans ces cas-là, comme ici, on applique le règle N + 1 de manière séquentielle. La Figure 10.26 (Vollhardt p.354) donne des exemples de profil de fragmentation qui peuvent être observés dans un tel cas selon les valeurs de Jab et Jbc. L’ordre de la séquence n’a pas d’importance (10.26), seulement des valeurs des constantes de couplage. Lorsqu’elles sont presque identiques, il peut en résulter des profils trompeusement simples.
Revenons maintenant au problème des alcools (Figure 10.15a). Pourquoi n’existe-t-il aucun couplage entre l’hydrogène hydroxyle (en vert sur la figure) et les hydrogènes du CH2 (en bleu). Simplement parce que dans les conditions de l’enregistrement du spectre RMN, il se produit des échanges rapides d’hydrogènes à la fois entre les molécules d’alcool et avec les traces d’eau. Cette vitesse rapide de l’ordre de 105 échanges par seconde implique que chaque hydrogène hydroxyle individuel ne passe qu’environ 10
ms dans le voisinage d’un oxygène donné. ce temps de liaison étant trop court, il ne se produit aucun couplage dans l’échelle de temps de la RMN. Les interconversions des orientations étant trop rapides, elles fusionnent en un seul déplacement chimique, et donc un seul pic. Une argumentation similaire est valable pour expliquer l’absence de scission pour le CH2.On dit de telles absorptions qu’elles sont découplées par les échanges de protons. Ces échanges peuvent être ralentis en enlevant toute trace d’eau, ou en refroidissant l’échantillon, comme il est montré à la Figure 10.28 (Vollhardt p.356) pour le méthanol.
En résumé, nous pourrons extraire d’un spectre RMN de protons les importantes informations suivantes:
1° Le déplacement chimique (
d) d’un pic nous renseigne sur l’environnement chimique du proton (la nature de l’atome lié à l’hydrogène)2° L’intégration du pic, ou l’aire (A) sous la courbe, ou la surface du pic nous renseigne sur le nombre de protons que l’on retrouve à cet endroit.
3° La multiplicité (M) (ou nombre) du pic nous renseigne sur le nombre de protons voisins non équivalents couplés (non isolés) par la multiplicité, i.e. le nombre de pics et suivant la règle de N + 1.
4° Les constantes de couplage (J) nous permettent d’attribuer les hydrogènes voisins responsables de la multiplcité d’un pic selon JAB=JBA.
5° Les pics d’un multiplet sont biaisés
(![]() ) dans la
direction de la fréquence de résonnance de noyaux responsables de la scission
en multiplet.
) dans la
direction de la fréquence de résonnance de noyaux responsables de la scission
en multiplet.
| Vollhardt, Chapitre 10, Problème 15 a,b,c |
6.1.6. RMN du carbone 13 (Vollhardt 10.9)
La RMN du
13C est potentiellement plus performante que celle du proton, parce que par définition, TOUS les composés organiques possèdent du carbone. Avec la RMN du 1H, ces deux techniques complémentaires fournissent des outils d’analyse puissants.Malheureusement, comme le montre le Tableau 10.1 (Vollhardt p.330) l’isotope naturel 12C es inactif en RMN et l’abondance naturelle du 13C est très faible, 1.11%. Le 13C réagira comme le
1H au champs magnétiques et on s’attendra à observer des spectres similaires. Toutefois, certaines différences importante (et utiles) différencient ces deux techniques.Premièrement, la résonance étant plus faible, les signaux du 13C sont environ 6000 fois plus faibles que ceux de 1H. En conséquence, les spectres devront être enregistrés par la technique de la transformée de Fourier dans le domaine du temps et convertis en spectres dans le domaine des fréquences. La description de cette technique dépasse le cadre du cours, mais il est important de noter qu’il est fréquent d’accumuler entre 10 000 et 100 000 spectres pour obtenir un RMN-13C.
Deuxièmement, à cause de la faible abondance des noyaux de 13C, il est très peu probable qu’un noyau donné possède un voisin 13C plutôt qu’un voisin 12C. Il en résulte une absence presque totale de couplage et les spectres de RMN-13C ne montrent que des singulets. Par contre, les noyaux 13C sont couplés avec les
1H voisins, et ceci doit être pris en ligne de compte. La Figure 10.29 (Vollhardt p.358) montre le RMN-13C du 1-bromoéthane. La valeur d=0 est mesurée par rapport du carbone dans le TMS. On peut voir que le couplage des protons donne un patron comportant un triplet et un quadruplet. On peut aussi voir que la fourchette des déplacements chimiques est plus large que celle observée pour l’hydrogène (environ 10 ppm). Cette fourchette peut s’étendre sur plus de 200 ppm (Tableau 10.6, Vollhardt p.359, et page suivante).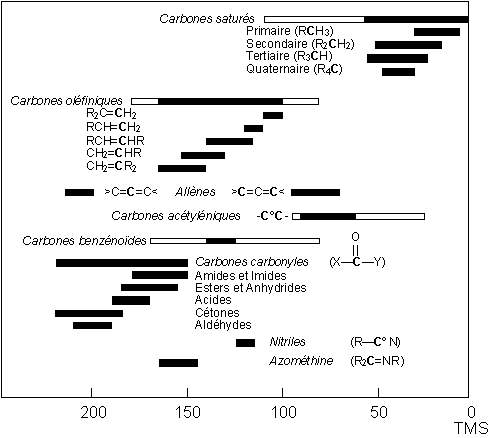
Il existe une technique qui permet de supprimer complètement le couplage 13C-1H: le découplage de bruit de fond (noise decoupled), ou découplage du proton en bande large. En résumé, on applique simultanément deux (2) fréquences sur l’échantillon. la première sert à provoquer la résonance des noyaux 13C, et la seconde sert à forcer tous les hydrogènes à résonner en même temps. il en résulte qu’aucun des noyaux de 13C ne peut distinguer d’état particulier ou ¯ des hydrogènes vicinaux. La conséquence est une absence totale de couplage. Il en résulte un spectre comme celui montré à la Figure 10.29 ou on montre le RMN-13C découplé du 1-bromoéthane, ou celui du phénylacétate d'éthyle:
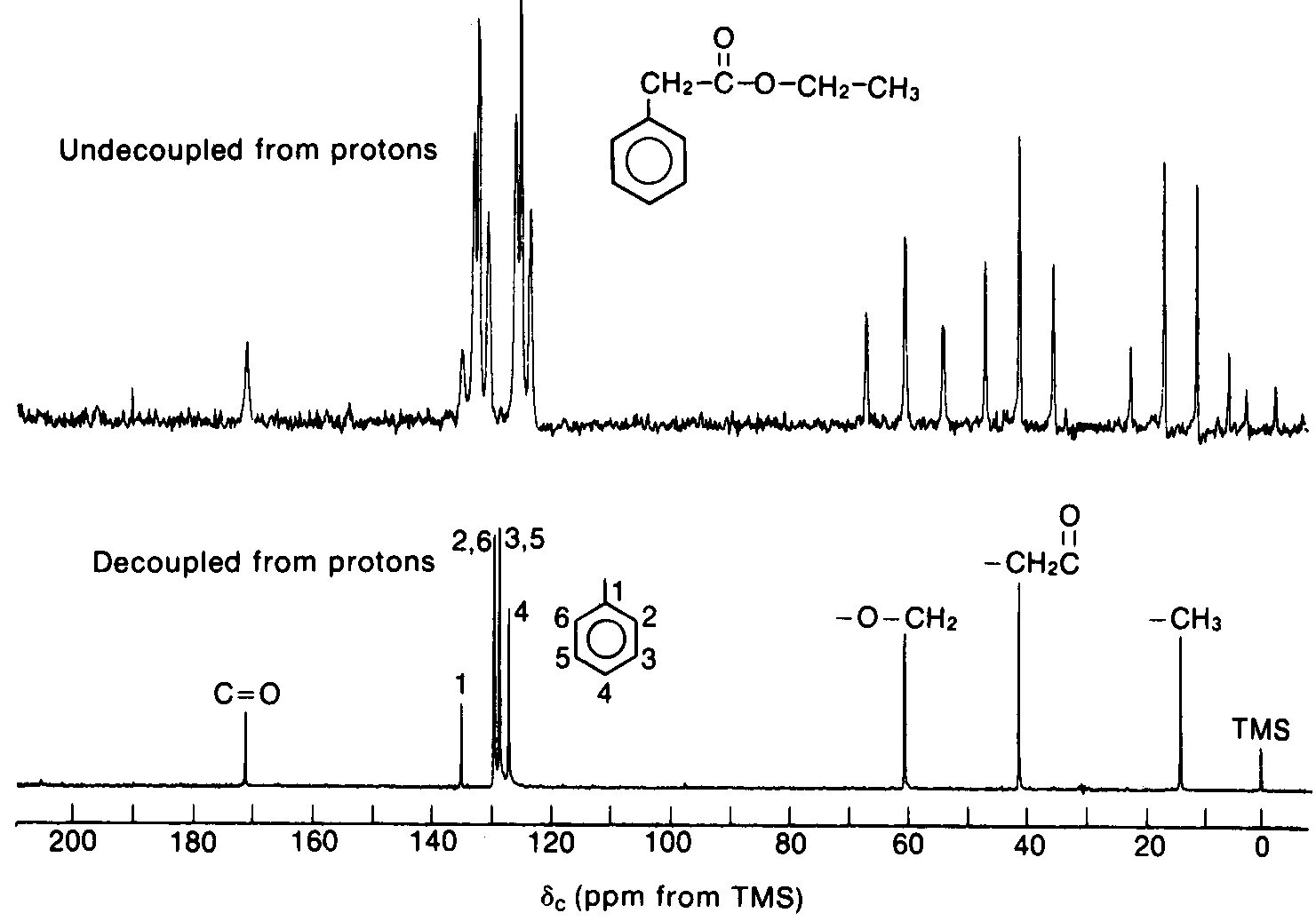
L’avantage de cette technique devient évidente lorsque l’on enregistre le spectre RMN-13C d’une molécule complexe: chaque atome de carbone possède un seul pic. Un tel exemple est montré à la Figure 10.31 (Vollhardt p.359) pour le méthylcyclohexane. On ne voit que 5 pics pour les 5 types de carbones différents.
Un autre exemple est la détermination aisée des isomères. Prenons le cas du C7H14. La Figure au haut de la p. 360 dans Vollhardt montre le nombres de pics associés a quelques-unes des structures possibles.
| Notions importantes aux pages 362 et 363 Encarts du chapitre 10 Tous les problèmes des pages 363 à 371 peuvent être faits, sauf évidemment ceux qui nécessitent un mécanisme réactionnel. Ceux qui demandent l’analyse de produits de réaction sans demander le mécanisme peuvent être faits. |
6.2. Spectroscopie U.V.-Visible et systèmes p délocalisés (Vollhardt 14.11, Pavia 5)
En spectroscopie U.V.-Visible, nous observons ce qui se passe lorsqu’un faisceau de lumière frappe une molécule. Lorsque certains groupements chimiques sont présents, ceux-ci vont absorber cette lumière. Cela se produit parce que le photon de lumière possède une énergie égale à l’énergie de transition des électrons impliqués dans la liaison chimique du groupement en jeu (Figure 14.13, Vollhardt p.535). Cette relation est:
D E = h
n =ou D E, la différence d’énergie est égale à h, la constance de Planck (6,626•10-34 J•s) multipliée par
n, la fréquence en Hertz, c est la vitesse de la lumière et l est la longueur d’onde. Les divers types de transitions possibles sont montrées à la Figure 14.14 (Vollhardt p.536).Une liaison simple, ne possédant que des électrons
s, absorbe la lumière d’une transition s® s* dans l’ultraviolet lointain au-dessous de 200 nm. Dans cette région, il est presque impossible d’effectuer des mesures correctes et précises, simplement à cause du grand nombre de liaisons qui absorbent dans cette région.Par contre, les transitions
p® p* et les transitions n® p* sont beaucoup moins énergétiques et peuvent être observées dans le domaine du proche ultraviolet et du visible.
Dans la région de 200 à 400 nm on observe surtout les électrons p délocalisés et les doublets libres des atomes comme O et N.
Absorptions typiques de chromophores simples et isolés
|
Classe |
Transition |
l max(nm) |
log e |
Classe |
Transition |
l max(nm) |
log e |
|
R—OH |
n ® s* |
180 |
2.5 |
R—NO2 |
n ® p* |
271 |
<1.0 |
|
R—O—R |
n ® s* |
180 |
3.5 |
R—CHO |
p ® p* |
190 |
2.0 |
|
R—NH2 |
n ® s* |
190 |
3.5 |
n ® p* |
290 |
1.0 |
|
|
R—SH |
n ® s* |
210 |
3.0 |
R2CO |
p ® p* |
180 |
3.0 |
|
R2C=CR2 |
p ® p* |
175 |
3.0 |
n ® p* |
280 |
1.5 |
|
|
R—C +C—R |
p ® p* |
170 |
3.0 |
RCOOH |
n ® p* |
205 |
1.5 |
|
R—C +N |
n ® p* |
160 |
<1.0 |
RCOOR' |
n ® p* |
205 |
1.5 |
|
R—N=N—R |
n ® p* |
340 |
<1.0 |
RCONH2 |
n ® p* |
210 |
1.5 |
Lorsque l’on augmente le nombre de liaisons doubles et que celles-ci sont conjuguées (chapitre suivant) comme dans le cas du
b-carotène: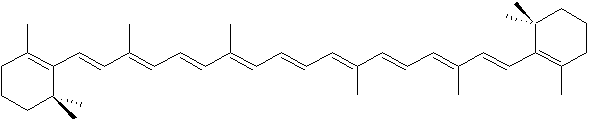
alors l’énergie des électrons
p diminue et le maximum d’absorption se déplace vers le domaine du visible passant par le violet, le bleu vers le vert, le jaune, l’orange et éventuellement le rouge.La Figure 14.15 (Vollhardt p.536) montre un exemple typique de spectre U.V.-Visible. Un pic dans un tel spectre est caractérisé par sa longueur d’onde,
l, exprimée en nm et son intensité caractérisée par son coefficient d’extinction molaire, e. Pour les solutions diluées, on peut évaluer la valeur de e par la loi de Beer-Lambert:A =
e ´ b ´ Cou l’absorbance, A, est proportionnelle au coefficient d’extinction molaire,
e, à la longueur du parcours optique en cm, b, et à la concentration, C.De plus, à cause des transitions impliquant les divers niveaux vibrationnels, les spectres U.V.-Visible présentent des bandes larges et non des pics étroits comme en RMN.
Les spectres U.V.-Visible nous révèlent l’étendue de la conjugaison des molécules organiques. En effet, l’ajout de doubles liaisons conjuguées, de même que de divers groupes fonctionnels augmente la valeur de
e et le déplacement bathochrome des pics (Tableau 14.2, Vollhardt p.538).Certaines molécules donnent lieu à des spectres électroniques complexes, tel l’azulène (Figure 14.16, Vollhardt p.537). Ce produit est de couleur violette, car il absorbe principalement les couleurs allant du vert au rouge dans le spectre, et ne réfléchit que les couleurs bleue et violet (règle de Woodward-Fieser).
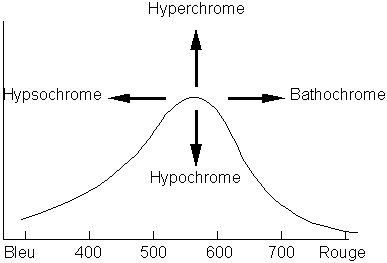
À quoi cela est-il dû? Lorsque le degré de conjugaison augmente, le nombre de niveaux d’énergie correspondant aux orbitales moléculaires
p augmente, et la différence d’énergie entre ceux-ci diminue (Figure 14.17, Vollhardt p.539). La transition HOMO-LUMO s’en trouve donc favorisée. HOMO signifie Highest energy Occupied Molecular Orbital, l’orbitale moléculaire occupée de plus haute énergie, et LUMO signifie Lowest energy Unnoccupied Molecular Orbital, l’orbitale moléculaire vide de plus basse énergie. Nous n’entrerons pas plus loin dans le détail de ces transitions, car cela dépasse le cadre du cours.L’analyse poussée de ces spectres par la position du maximum du pic et par sa valeur de
e nous permet de différencier la présence de systèmes aromatiques, de cétones, d’acides et de polyènes conjugués.| Notion importante 14 à la p.542 Les problèmes 29-30 des pages 542 à 548 peuvent être faits. |
6.3. Spectroscopie infrarouge (Vollhardt 11.5 et Pavia 2)
En spectroscopie infrarouge, ce que nous observons ce n’est pas la transition des électrons, mais plutôt l’énergie associée à la vibration de la liaison comme des boules reliées par des ressorts. On peut même démontrer que la fréquence de vibration entre deux atomes dépend de la force de la liaison qui les unit et de leur masses atomiques respectives selon la loi de Hooke (qui décrit les mouvements d’un ressort):
![]()
ou = fréquence vibrationnelle en nombres d’ondes (cm
-1), k = constante, f = constante de force, indiquant la raideur du ressort (de la liaison), m1 et m2 = les masses attachées au ressort (masses des atomes unis).Les valeurs de longueur d’onde des spectres IR vont de 2 à 15
m. Cependant, l’usage veut que l’on caractérise un rayonnement IR non pas par sa longueur d’onde ou sa fréquence, mais par le nombre d’onde selon:n barre = 1 /
lPar exemple, 5
m = 5•10-4 cm ® = (5•10-4)-1 = 2 000 cm-1.Chaque type de liaisons possède une fréquence de vibration propre. Le spectre IR est donc extrêmement important par son habilité à identifier les groupements. Certains d’entre eux possèdent une fréquence extrêmement caractéristique qui permet de les identifier à coup sur, comme -OH et C=O.
Un exemple est donné à la Figure 11.17 (Vollhardt p.390) pour le cyclohexanol. On peut y voir les massifs responsables des divers types d’absorption. On peut voir que le spectre est complexe et résulte d’autres facteurs comme les divers modes de vibrations (Figure 11.13, Vollhardt p.388).
| Démonstration des vibrations d’élongation, et de déformation symétriques, asymétriques et de balancement d’un atome de carbone tétraédrique |
Il est important de noter que les divers groupes fonctionnels donnent lieu à des absorption infrarouges caractéristiques comme le montre le Tableau 11.3 (Vollhardt p.388). Il existe même une région du spectre située entre 600 et 1500 cm-1 que l’on appelle la région de l’empreinte digitale. Cette région est très caractéristique et sert à l’identification des composés lorsque comparés avec un base de donnée sur ordinateur.
Lorsque nous verrons les divers groupements fonctionnels, l’étudiant est
invité à revenir voir ce tableau 11.3.
Toutefois, les spectres IR sont généralement très complexes et on doit se rappeler qu’il est pour ainsi dire impossible d’attribuer toutes les bandes d’absorption dans un tel spectre. On doit se contenter des bandes principales, tant par leur présence que par leur absence. Ces principales bandes sont identifiées dans le Tableau 11.3, et on doit connaître tout particulièrement les bandes des groupements alcools, cétones, amines et alcènes.
|
Notions importantes 5 et 6 aux p.403-404. |
6.4. Spectrométrie de masse (Vollhardt 20.9 et Pavia 6)
En spectrométrie de masse, un échantillon est introduit dans une enceinte sous vide, vaporisé puis soumis au bombardement d’un canon à électrons de grande énergies (Figure 20.4, Vollhardt p.797). Un électron est arraché aux molécules et on obtient une espèce qui est à la fois un cation (ion positif) et un radical libre (nombre impair d’électrons) que l’on appelle ion moléculaire.
M + e
- (70 eV) ® M+• + 2 e-À cause de l’énergie du faisceau ionisant, l’ion moléculaire va se fragmenter par la rupture de certaines liaisons pour donner des ions positifs de masse plus faible, qui pourront se fragmenter à nouveau. Ce phénomène donne naissance à une foule de pics supplémentaires, tous de masse inférieure à celle de l’ion moléculaire (appelé aussi ion parent). Expérimentalement, on observe donc un diagramme de fragmentation.
Ces ions sont ensuite accélérés dans un champ électrique, puis dirigés entre les pôles d’un aimant selon une trajectoire circulaire qui dépend de leur rapport m/z (ou m/e), i.e. celui de leur masse à leur charge. Ils seront ainsi déviés et dirigés vers un détecteur. En faisant varier le champ électrique, on fait ainsi varier la vitesse des ions moléculaires et donc leur vitesse, on peut les faire parvenir au détecteur par ordre croissant de rapport m/z. Étant donne que z (e) est pratiquement toujours à 1, on obtient une mesure de la masse de tous les fragments et de la molécule initiale.
Dans un spectre de masse, comme celui du méthane montré à la Figure 20.5 (Vollhardt p.798) la hauteur relative des pics indique l’abondance relative des espèces, et dons donne une indication de la facilité relative de leur formation.
Il est bon de se rappeler que la masse de l’ion moléculaire est aussi la masse moléculaire de la molécule intacte.
Une caractéristique inusitée est la présence d’un petit pic (1.1%) à m/z= 17. ce pic est désigné par (M+1)
+•. D’où vient-il? On doit se rappeler que le carbone n’est pas isotopiquement pur et qu’il continent environ 1.1% de 13C. En plus de nous permettre la RMN-13C, on voit que la présence des isotopes, comme 13C, peut être détectée par spectrométrie de masse. L’isotope de l’hydrogène, le deutérium, possède une abondance naturelle de 0.015 %, et est pour ainsi dire nulle. Toutefois, d’autres éléments présentent des isotopes plus aisément détectables (Figure 20.7, Vollhardt p.800) :|
Isotope |
15 N |
18 O |
33 S |
34 S |
35 Cl |
37 Cl |
79 Br |
81 Br |
|
Abondance (%) |
0.366 |
0.204 |
0.76 |
4.22 |
75.53 |
24.47 |
50.54 |
49.46 |
À la suite de l’ionisation, la fragmentation qui se produit se déroule selon des règles précises: les liaisons les plus faibles sont rompues avant les liaisons les plus fortes. Il en résulte l’apparition de pics caractéristiques (voir ci-après). Un exemple est donné aux Figures 20.8 à 20.10 (Vollhardt p.802) pour les trois isomères du pentane. Les diagrammes de fragmentation de ces trois composés sont différents, et donc les isomères sont parfaitement identifiables.
Les groupements fonctionnels présentent des profils particuliers de fragmentation. L’étude de ces procédés dépasse le cadre du cours, mais l’étudiant curieux peut lire les pages 803 à 808. Il est important de mentionner que chaque composé différent possède un diagramme de fragmentation qui lui est propre: cela constitue une sorte d’empreinte digitale du composé. Des ordinateurs permettent ainsi de déterminer la structure de ces molécules par la connaissance de tous ces diagrammes de fragmentation. C’est aussi pourquoi le spectromètre de masse est un des détecteurs les plus utilisés dans un chromatographe en phase gazeuse (GC/MS).
| Notions importantes 9-10 à la page 814 Encart 20.4 Les problèmes 27 à 30 des pages 814 à 822 peuvent être faits. |
Fragments ioniques communs de masse inférieure à 105 (m/e, Ions)
|
14 |
CH 2 |
15 |
CH 3 |
|
16 |
O |
17 |
OH |
|
18 |
H 2O; NH4 |
19 |
F; H 3O |
|
26 |
C +N |
27 |
C 2H3 |
|
28 |
C 2H4; CO; N2 (air); CH=NH |
29 |
C 2H5; CHO |
|
30 |
CH 2NH2; NO |
31 |
CH 2OH; OCH3 |
|
32 |
O 2 (air) |
33 |
SH; CH 2F |
|
34 |
H 2S |
35 |
Cl |
|
36 |
HCl |
39 |
C 3H3 |
|
40 |
CH 2C=N |
41 |
C 3H5; CH2C=N + H; C2H2NH |
|
42 |
C 3H6 |
43 |
C 3H7; CH3C=O; C2H5N |
|
44 |
CH 2CH=O + H; CH3CHNH2; CO2; NH2C=O; (CH3)2N |
45 |
CH 3CHOH; CH2CH2OH; CH2OCH3; C(O)OH; CH3CH-O + H |
|
46 |
NO 2 |
47 |
CH 2SH; CH3S |
|
48 |
CH 3S + H |
49 |
CH 2Cl |
|
51 |
CHF 2 |
53 |
C 4H5 |
|
54 |
CH 2CH2C+N |
55 |
C 4H7; CH2=CHC=O |
|
56 |
C 4H8 |
57 |
C 4H9; C2H5C=O |
|
58 |
CH 3C(O)CH2 + H; C2H5CHNH2; C2H5NHCH2; C2H2S |
59 |
(CH 3)2NHCH2; (CH3)2COH; CH2OC2H5; CH3OC=O; NH2C(O)CH2 + H; CH3OCHCH3; CH3CHCH2OH |
|
60 |
CH 2C(O)OH + H; CH2ONO |
61 |
CH 3OC=O + 2H; CH2CH2SH; CH2SCH3 |
|
65 |
|
66 |
|
|
67 |
C 5H7 |
68 |
CH 2CH2CH2C+N |
|
69 |
C 5H9; CF3; CH3CH=CHC=O; CH2=C(CH3)C=O |
70 |
C 5H10 |
|
71 |
C 5H11; C3H7C=O |
72 |
C 2H5C(O)CH2; C3H7CHNH2; (CH3)2N=C=O; C2H5NHNHCH3 et isomères |
|
73 |
Homologues de 59 |
74 |
CH 2C(O)OCH3 + H |
|
75 |
C 2H5OC=O + 2H; CH2SC2H5; (CH3)2CSH; (CH3O)2CH |
77 |
C 6H5 |
|
78 |
C 6H5 + H |
79 |
C 6H5 + 2H; Br |
|
80 |
CH 3SS + H |
81 |
C 9H9; Br;
|
|
82 |
CH 2CH2CH2CH2C+N; CCl2; C6H10 |
83 |
C 6H11; CHCl2 |
|
85 |
C 6H13; C4H9C=O; CClF2 |
86 |
C 3H7C(O)CH2 + H; C4H9CHNH2 et isomères |
|
87 |
C 3H7C(O)O; CH2CH2C(O)OCH3; Homologues de 73 |
88 |
CH 2C(O)OC2H5 + H |
|
89 |
C 3H7OC=O + 2H;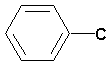
|
90 |
CH 3CHONO2;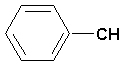
|
|
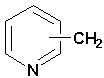
91 |
(CH 2)4Cl;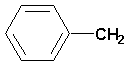 ; ; 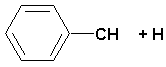 ; ;
 ; ; 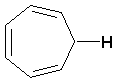 ; ;
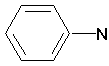
|
92 |
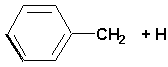
|
|
93 |
CH 2Br; C7H9;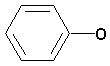
|
94 |
|
|
96 |
CH 2CH2CH2CH2CH2C+N |
97 |
C 7H13 |
|
99 |
C 7H15; C6H11O |
100 |
C 4H9C(O)CH2 + H; C5H11CHNH2 |
|
101 |
C 4H9OC=O |
102 |
CH 2C(O)OC3H7 + H |
|
103 |
C 4H9OC=O + 2H; C5H11S; CH(OCH2CH3)2 |
104 |
C 2H5CHONO2 |
|
105 |
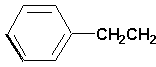 ; ; 
|
| Retour au menu |
|
ABCSITE © copyright 2000 |