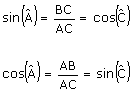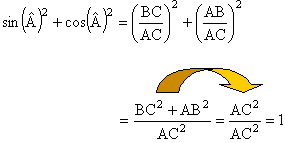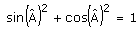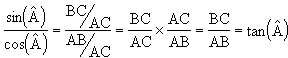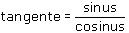Droites d'un triangle

triangle rectangle

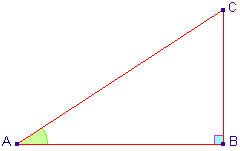
Au collège, sont introduites les notions de sinus, cosinus et tangentes. A la différence de ce qui est fait dans MATHilde Seconde, celles-ci ne se rapportent qu'à des angles géométriques, c'est-à-dire des réels positifs.
En fait, on peut dire qu'en Seconde, on prolonge ce qui est fait au collège...

Sinus, cosinus et tangente d'un angle.

Définition : (sinus, cosinus et tangente)
ABC est un triangle rectangle en B. Le sinus de l'angle est le rapport des longueurs du côté opposé à cet angle et de l'hypoténuse.

Le cosinus de l'angle est le rapport des longueurs du côté adjacent à cet angle et de l'hypoténuse.

La tangente de l'angle est le rapport des longueurs du côtés opposé et adjacent à cet angle et de l'hypoténuse.

Remarque : il arrive que l'on parle du cosinus de 55°. En fait, c'est un abus de langage. Il serait plus correct de dire "cosinus d'un angle de 55°".
Mais est-ce si important ?

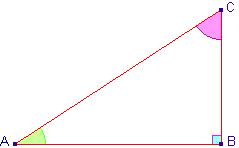
Propriétés des sinus, cosinus et tangente.
Ces trois fonctions présentent certaines propriétés que nous allons énoncer :

En tant que rapport de deux longueurs, les sinus et cosinus d'un angle sont des nombres positifs. Ils sont donc plus grand que 0.
De plus, dans un triangle rectangle, le plus grand côté est l'hypoténuse. Les sinus et cosinus d'un angle sont donc plus petit que 1.
En conséquence :

Propriété 1 : les sinus et cosinus d'un angle sont compris entre 0 et 1.

Si dans un triangle rectangle, on connaît les sinus et cosinus d'un premier angle non droit alors il est possible de déterminer les mêmes choses pour le second angle non droit.

Propriété 2 : si ABC est un triangle rectangle en B alors :

Qui dit triangle rectangle, dit théorème de Pythagore. Celui permet de lier dans une égalité les carrés des sinus et cosinus. Illustration.

Dans le cas ci-contre :
Comme le triangle ABC est rectangle en B, alors en application du théorème de Pythagore :
AB² + BC² = AC²
Ainsi :

Propriété 3 : la somme des carrés des sinus et cosinus d'un même angle est égal à 1.

Enfin dernière propriété : lorsque l'on connaît les sinus et cosinus d'un angle, on a de facto sa tangente. Illustration :
Tout repose sur les définitions des sinus, cosinus et autre tangente.

Propriété 4 : la tangente d'un angle est le quotient de ses sinus et cosinus.

Retour menu

Remonter