|
Les quatre transformations définies ci-dessous ont déjà été vues,
définies et pratiquées au collège. Dans cette page, nous nous
bornerons à en rappeler les vraies définitions ainsi quelques
propriétés qui seront illustrées.
Symétrie centrale.
La symétrie centrale est la première transformation vue au
collège. Elle se fait par rapport à un centre, c'est-à-dire par
rapport à un point.
|
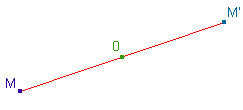
Définition : dire que le point M' est l'image du
point M par la symétrie de centre O
signifie que O est
le milieu du segment [MM'].
 |
Note : la symétrie centrale est une
homothétie de rapport -1. C'est aussi une rotation de p radians ou
180° e
Les propriétés de cette symétrie centrale sont les suivantes :
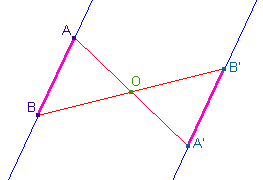
| A' et B' sont les images
respectives des points A et B par la symétrie de centre
O.
L'image de la droite (AB) par la symétrie de centre O
est la droite (A'B'). De plus, ces deux droites sont
parallèles.
De la même façon, l'image du segment [AB] par cette
même symétrie de centre O est le segment [A'B'].
Enfin, la symétrie centrale est une isométrie.
C'est-à-dire qu'elle conserve les longueurs. Ainsi :
AB = A'B'. |
 |
La symétrie centrale conserve aussi le parallélisme et
l'orthogonalité. Donc :
| La symétrie centrale
conserve également les angles géométriques et
orientés.
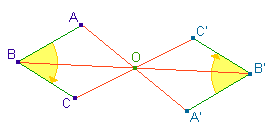
Ainsi si A', B' et C' sont les images respectives des
points A, B et C par la symétrie ce centre O alors
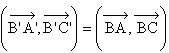 . . |
 |
La symétrie centrale conserve donc les formes et les figures : un
triangle rectangle ou isocèle reste rectangle ou isocèle, un
quadrilatère demeure un quadrilatère, les carrés restent des
carrés... etc...
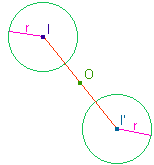
| Dans le même esprit,
ajoutons que la symétrie centrale conserve les cercles.
Si I' est l'image du point I par la symétrie de
centre O alors l'image du cercle de centre I et de
rayon r par cette même symétrie est le cercle de
centre I' et de rayon r. |
 |
Symétrie axiale.
La symétrie axiale se fait par rapport à un axe, c'est-à-dire
par rapport à une droite.
Définition : dire que le point M' est l'image du
point M par la symétrie d'axe ( )
signifie que
la droite D est la médiatrice
du segment [MM']. )
signifie que
la droite D est la médiatrice
du segment [MM'].
 |
Passons en revue (ga'd'vô !) les propriétés de cette symétrie
axiale.
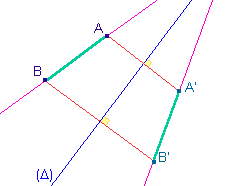
| Comme pour sa consoeur
centrale, la symétrie axiale conserve alignement et
longueur.
Si A' et B' sont les images respectives des points A
et B par la symétrie d'axe (D)
alors :
- L'image de la droite (AB) par celle-ci est la
droite (A'B').
Mais ces deux droites ne sont pas nécessairement
parallèles.
- L'image du segment [AB] est le segment [A'B'].
- La longueur A'B' est égale à la longueur AB.
|
 |
La symétrie axiale conserve aussi le parallélisme,
l'orthogonalité, les formes et les figures. De même, l'image d'un
cercle est un cercle de même rayon.
Seule grande différence avec la "centrale", si elle conserve les
angles géométriques, elle inverse les angles
orientés.
Si A', B' et C' sont les
images respectives des points A, B et C par la symétrie
d'axe (D) alors
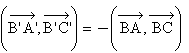 . .
Par contre, les angles géométriques correspondant sont
égaux. |
 |
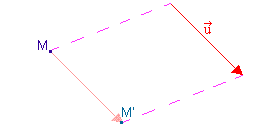
Translation.
La translation est l'appellation mathématique de ce que l'on
appelle communément un déplacement.
Lorsque l'on se déplace, on fait mouvement dans une certaine
direction et d'une certaine distance : autrement dit, on se déplace
selon un certain
vecteur.
La translation déplace les figures et les situations
géométriques. Cette transformation a donc certainement toutes les
"vertus".
Examinons donc les propriétés de la translation.
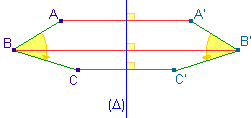
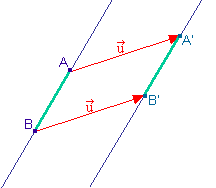
A' et B' sont les images
respectives des points A et B par la translation de
vecteur
 . .
L'image de la droite (AB) par cette translation est
la droite (A'B'). De plus, ces deux droites sont
parallèles.
L''image du segment [AB] est le segment [A'B'].
Enfin, la translation est aussi une isométrie. Les
longueurs AB et A'B' sont donc égales. |
 |
La translation conserve aussi tout ce qui est parallélisme et
orthogonalité. Ainsi les carrés demeurent-ils des carrés, des
cercles restent des cercles...
Reste à voir ce qu'il advient des angles orientés ou non.
| Puisqu'elle les
déplace, la translation conserve donc les angles et
orientés.
Si A', B' et C' sont les images respectives des
points A, B et C par la symétrie ce centre O alors
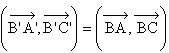 . . |
 |
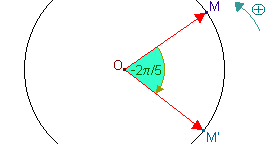
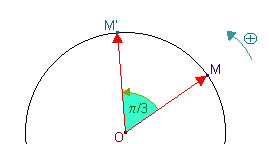
Rotation.
Une rotation fait pivoter les figures ou les formes autour d'un
point.
Cette pauvre bougresse est introduite en Troisième. La
description qu'on en donne la bâtardise. Nous allons rétablir cette
ignominie.
La définition que nous donnerons de la rotation s'appuie sur les
angles orientés.
Enfin si en Troisième les angles sont donnés en degrés, en Seconde
et après ils sont exprimés en
radians.
Une rotation de p radians ou
180° est une symétrie centrale.
La rotation fait pivoter les figures et les situations
géométriques. A l'instar de ces trois consœurs, cette
transformation conserve donc tout ! Mais voyons cela en détail !
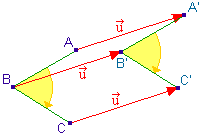
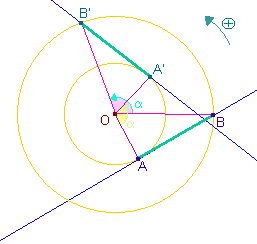
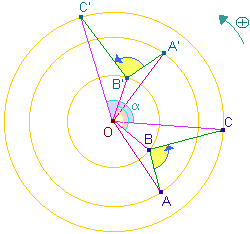
| A' et B' sont les images
respectives des points A et B par la rotation de centre
O et d'angle a.
L'image de la droite (AB) par ladite rotation est la
droite (A'B'). Cependant ces deux droites ne sont pas
nécessairement parallèles.
L''image de [AB] est le segment [A'B'].
Enfin, la rotation est aussi une isométrie. Elle
conserve donc les distances . |
 |
A l'instar des trois précédentes transformations, la rotation
conserve parallélisme, la perpendicularité, les formes et les
figures.
| Elle conserve également
les angles
orientés.
Ainsi si A', B' et C' sont les images respectives des
points A, B et C par la rotation de centre O et d'angle
a alors
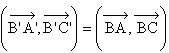 . . |
 |
|
 Retour
menu
Retour
menu

![]()


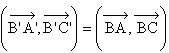 .
.

 )
signifie que
la droite D est la médiatrice
du segment [MM'].
)
signifie que
la droite D est la médiatrice
du segment [MM'].


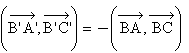 .
.