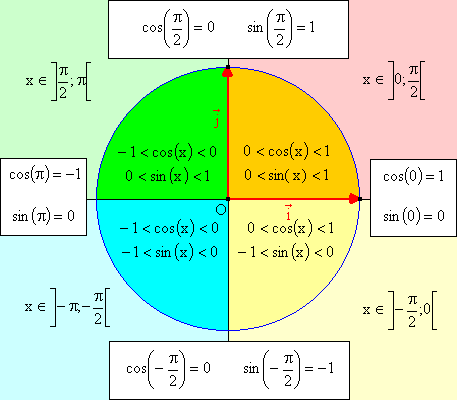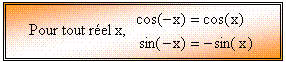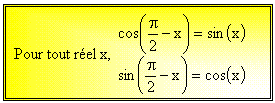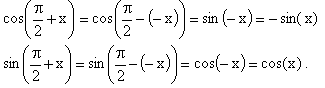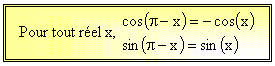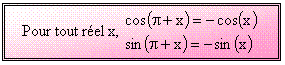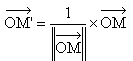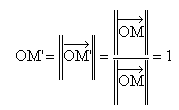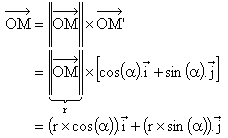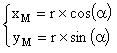Retour
menu |
 |
Droites d'un triangle |
|
|
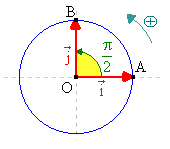
1°) Repères et bases directs et indirects.
Il va sans dire que les points A et B sont sur le cercle trigonométrique de centre O et de rayon 1.
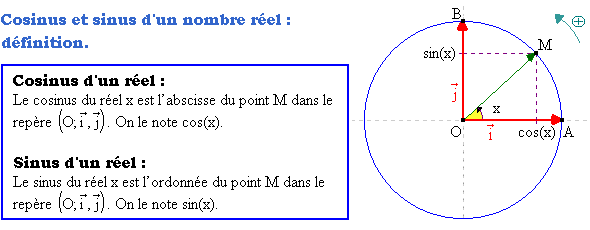
2°) Sinus et cosinus d’un nombre réel. x est un nombre réel. On note M le point du cercle trigonométrique associé au
réel x. C’est-à-dire que c’est l’angle orienté (
Pour manipuler sinus, cosinus et tangente, cliquer sur le bouton ci-dessous. Autrement dit, M a pour coordonnées (cos(x) ; sin(x)) ou
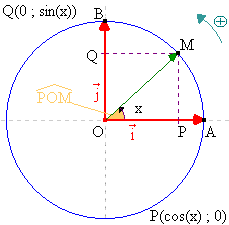
On appelle P le projeté orthogonale de M sur l’axe des abscisses et Q le projeté sur l’axe des ordonnées.
Remarquons que lorsque x Î [0 ;
Ceci car OM = 1. M est en effet un point du cercle trigonométrique. Autrement dit, cos(x) et sin(x) sont respectivement égaux aux cosinus et
cosinus de l’angle géométrique
Cosinus et sinus remarquables. Les sinus et cosinus de certains réels sont aisément calculables.
cos(0) = 1 et sin(0) = 0
cos(
Ainsi :
Comme P est le projeté orthogonal de M sur l’axe (O ;
En remplaçant, il vient que :
Soit x un nombre réel tel que cos(x) ¹ 0 alors la tangente du réel x est le quotient de son sinus et de son cosinus. On la note :
Si on appelle
Signe du sinus et du cosinus. Le sinus et le cosinus de tout nombre réel font partie de l’intervalle [-1 ; 1]. Plus précisément, la position de M nous permet d'en savoir plus sur le cosinus et le sinus de x. Ainsi :
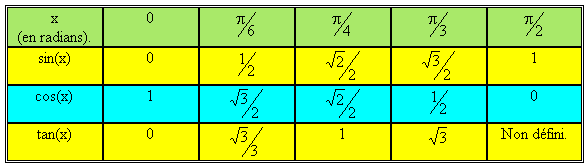
Cosinus, sinus et tangente d’angles remarquables. Il est possible de calculer certains sinus, cosinus et tangente à partir de situations géométriques particulières. Le tableau suivant les récapitule. Pour savoir pourquoi il en est ainsi, cliquer sur la case souhaitée.
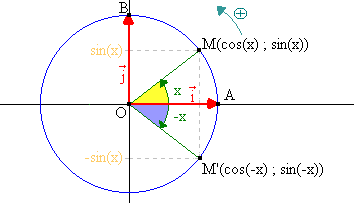
On appelle M' le point associé au réel –x. Il a donc pour coordonnées (cos(-x) ; sin (-x)).
M' est le symétrique de M par rapport à l'axe des abscisses. Ces deux points ont donc des abscisses égales mais des ordonnées opposées. Ainsi :
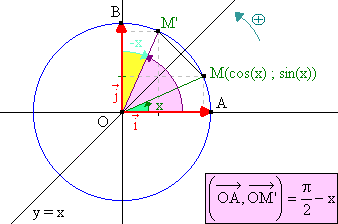
M est toujours le point du cercle trigonométrique associé au réel x. On note
M’ le point associé au réel
Remarquons qu’alors M’ est le symétrique de M par rapport à la droite d’équation y = x. C'est celle que l'on appelle la première bissectrice du plan. On montre qu'alors l'abscisse du point M' est égale à l'ordonnée de M et que l'abscisse de ce dernier est l'ordonnée de ce premier. Ainsi :
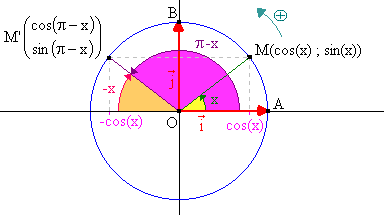
Intéressons-nous maintenant aux cosinus et sinus de
Ainsi donc :
Cosinus et sinus de On appelle M’ le point associé au réel
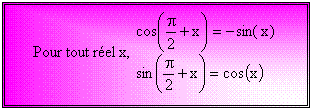
On remarque alors que M' est le symétrique de M par rapport à l'axe des ordonnées. Ces deux points ont donc des ordonnées égales mais des abscisses opposées. Ainsi :
Intéressons-nous maintenant à
Ainsi :
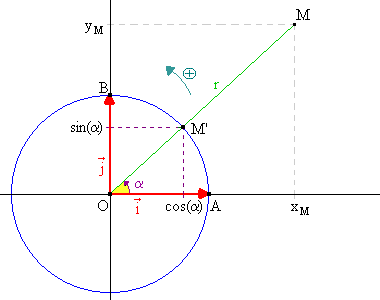
L'extra-plus : coordonnées polaires. Ce dont nous parlerons dans ce paragraphe est largement hors programme. C'est seulement qu'à présent que nous savons beaucoup de choses, il serait stupide de s'arrêter ! Dans le repère orthonormé direct qu'est (O ;
Soit donc M un point du plan. On appelle alors M' le point défini par :
Remarquons que M' fait partie du cercle trigonométrique (c'est-à-dire le cercle de centre O et de rayon 1). En effet :
Il existe donc un unique réel a Î ]-
Le point M est donc parfaitement repéré par le couple de réels (r , a ) comme il l'est d'ailleurs par le couple (xM ; yM). On parle pour ce premier de coordonnées polaires et pour ce dernier de coordonnées cartésiennes. La dernière relation vectorielle nous permet enfin d'écrire que :
|
, 
) a pour mesure x radians.
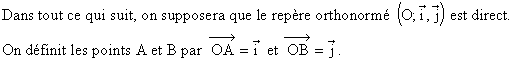
/2] alors 
.
Si x = 0 alors le point du
cercle trigonométrique associé à x est le point A(1 ; 0). Ainsi : 
, 
), le point P a pour coordonnées
(cos(x) ; 0) et le point Q(0 ; sin(x)). 
.
.
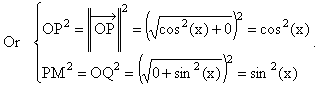la tangente au cercle
trigonométrique en A alors le couple (1 ; tan(x)) est les coordonnées du point
d’intersection des droites (OM) et 
