|
Globalement, trois grands théorèmes sont vus au
collège :
-
Le théorème de Thalès et son dérivé celui des
milieux.
-
Le théorème de Pythagore.
-
Le théorème de l'angle au centre.
L'objet de cette page est de les rappeler et de
proposer une démonstration.
Théorème de Thalès et théorème des milieux.
Ce que nous appellerons le théorème de Thalès est en fait le
théorème proprement dit et sa réciproque.
Le théorème constitue une première et importante étape dans la
"numérisation" de la géométrie : une égalité de rapport implique un
parallélisme. Comme chacun peut le constater, il est plus facile de
raisonner sur des nombres que sur des points ou des droites...
Théorème : (de
Thalès)
A, B, C sont trois points du plan.
Le point M fait partie de la droite (AB).
Le point N fait partie de la droite (AC).
- Si les droites
(BC) et (MN) sont parallèles
alors
 .
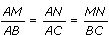- Si on a
l'égalité
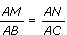et si les deux triplets de points A ,B, M et A, C,
N s'enchaînent dans le même ordre
alors les
droites (BC) et (MN) sont parallèles.
|
 |
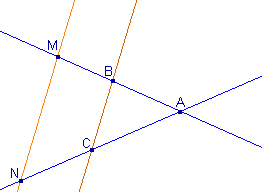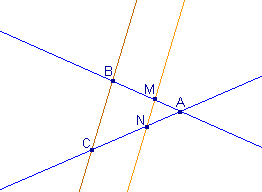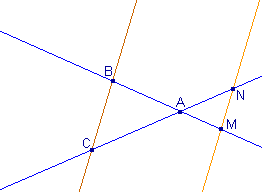Il existe une version
vectorielle du théorème de Thalès. C'est à partir de celle-ci
que le théorème ci-dessus peut-être démontré.
Un peu d'histoire
: Thalès était un savant grec qui vécut entre -627
et -547. Originaire de la ville de Milet, il était un
généraliste des sciences comme la majorité de ses
confrères de l'époque.
La propriété comme quoi la proportionnalité des
longueurs et le parallélisme sont liés, est connue et
employée depuis l'antiquité. Le théorème de Thalès ne
serait pas dû à la personne dont il porte le nom. Ce
sont en fait des français qui le baptisèrent ainsi à la
fin du XIXème siècle. |
Un des corollaire du théorème de Thalès est le théorème des
milieux. Même si ce dernier était connu sans doute bien avant
l'énoncé de Thalès, il n'en demeure pas moins un cas particulier.
Même si la formulation que nous en donnerons ne le laisse pas
transparaître.
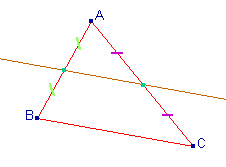
Théorème : (des milieux)
- La droite qui
passe par les milieux de deux des côtés du triangle
est parallèle au troisième côté.
- Si une droite
passe par le milieu d'un premier côté et est
parallèle au second côté
alors elle passe également par le milieu
du troisième côté.
|
 |
Théorème de Pythagore.
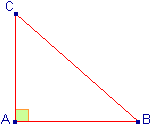
Théorème : (de Pythagore)
A, B et C sont trois points du plan.
Dire que le triangle
ABC est rectangle en A
équivaut à dire que AC2 + AB2
= BC2 |
 |
Ce théorème permet de démontrer qu'un triangle dont
l'on connaît les dimensions, est rectangle.
Il permet aussi de déterminer la longueur du troisième côté d'un
triangle rectangle pour peu que l'on en connaisse les longueurs des
deux premiers.
| Un peu d'histoire
: le théorème de Pythagore était connu des
Babyloniens dés 1500 avant que Jésus n'est Crié.
Cependant, le premier à l'avoir démontré est un certain
Pythagore (né en -580, mort en -500) originaire de la
ville de Samos (Grèce). Depuis ce théorème porte son
nom. |
Théorème de l'angle au centre.
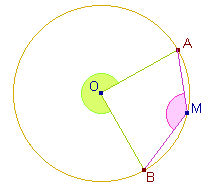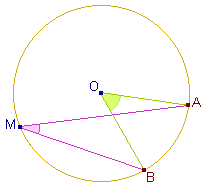
Théorème : (de
l'angle au centre)
A et B sont deux points d'un cercle de centre O.
Pour tout point M de
ce cercle, la mesure de l'angle géométrique
AMB est égale à la
moitié de celle de l'angle au centre
AOB. |
 |
 |
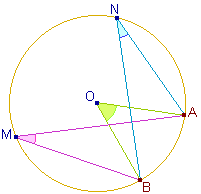Une des conséquences de ce théorème est que si M et
N sont deux points du cercle de centre O alors les
mesures des angles
AMB et
ANB sont égales.
En effet, ils sont toutes les deux égales à la moitié
de l'angle au centre
AOB. |
|
Retour
menu
