|
Tout au long de son mathématique périple, le collégien apprend à construire
un triangle, puis il y trace des droites particulières qui sont toutes
concourantes. Au travers de cette page, nous allons récapituler tout ce qui a
été vu durant ces quatre années (ou plus).
Hauteurs et orthocentre.
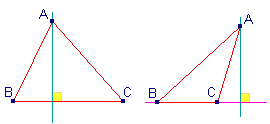
| La hauteur du triangle ABC issue du sommet A
est la droite qui passe par ce point et qui est perpendiculaire au côté
opposé (BC). |
 |
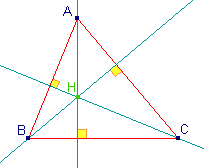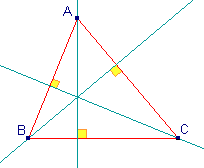 |
Dans un triangle, les trois hauteurs issues
des trois sommets sont concourantes (se coupent en un point H qui est
l'orthocentre du triangle. |
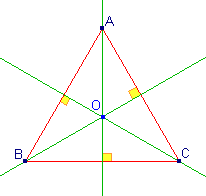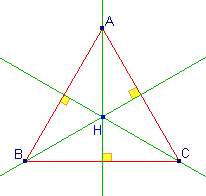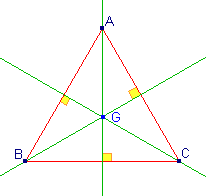
Médianes et centre de gravité.
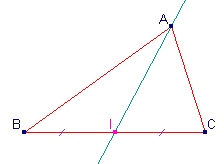
| La médiane du triangle ABC issue du sommet A
est la droite qui passe par A et par le milieu I du côté opposé [BC]. |
 |
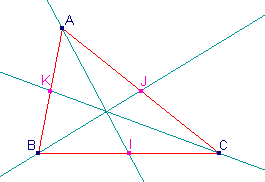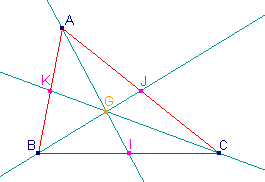 |
A l'instar des hauteurs, les trois médianes
d'un triangle sont concourantes en un point G qui est le centre de gravité
de ce triangle.
Une
relation vectorielle permet de caractériser ce point G.
A partir de celle-ci, on montre qu'il se trouve aux deux tiers de la
médiane [AI] en partant de A. |
Médiatrices et centre du cercle circonscrit.
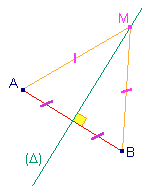
| La médiatrice n'est une chose spécifique à un
triangle mais plutôt à un segment. Néanmoins, un triangle a trois côtés et
donc, autant de ces droites.
La médiatrice du segment [AB] est la droite (D) qui coupe ce segment perpendiculairement en son
milieu.
C'est aussi l'ensemble des points du plan équidistants de A et
de B. |
 |
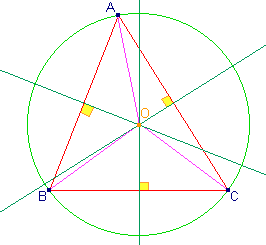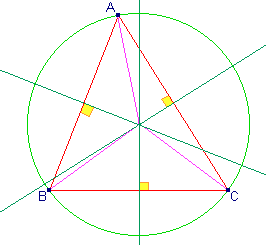 |
Les trois médiatrices d'un triangle sont
concourantes en un point O.
Ce point est situé à égales distances des
sommets de ce triangle.
Il est le centre du cercle circonscrit à ce
triangle, c'est-à-dire le centre du seul cercle qui passe par les trois
sommets du triangle. |
Triangles isocèle et équilatéral.
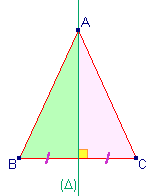
| Si le triangle ABC est isocèle en A (les deux
côtés égaux partent de ce sommet) alors la hauteur (D) issue de ce sommet A est aussi la médiatrice du côté
opposé [BC] et la médiane issue de A. |
 |
 |
On peut voir un triangle équilatéral comme
étant un "triple triangle isocèle".
Ainsi, dans un triangle équilatéral, la hauteur issue d'un sommet est
aussi la médiane issue de ce sommet ainsi que la médiatrice du côté
opposé. |
|
 Retour
menu
Retour
menu

![]()







