|
Série
6 (suite):
Air
humide
|
Exercice
3 :
Un cylindre de volume V1
= 2 dm3
fermé par un piston, contient initialement de l’air humide à la
température t1=15
°C, à la pression
P1 = 1 bar,
et à l’humidité relative j1
=
0,2 .
1-
Quelle
augmentation de pression isotherme
(piston lentement enfoncé dans le cylindre) faut-il faire
subir à cet air pour l’amener à la saturation ?.
2-
Calculer
la masse d’eau liquide par Kg d’air sec qui apparaît si la
variation de la pression réalisée est égale à
1,25 fois celle qui est juste suffisante pour provoquer la
saturation ?.
Solution
3 :
1-
A
l’état initial, on a : V1
= 2 dm3
, t1 =
15 °C , P1
= 1 bar , j1 = 0,2
A la saturation, on a : j
= 1
et DP = P2 – P1
Pour une transformation qui garde à l’état de vapeur toute
l’eau contenue dans le cylindre, on a
: mV
= cte d’où x
=
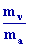= cte
Soit e2
l’état de saturation, lorsqu’il est atteint par
augmentation de pression isotherme sans qu’il y a production du
liquide,
on
a x1 = 0,622
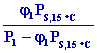or d’après
la table PS,15°C =
17,04 m bar
d’où
x1
= 0,622
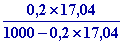= 0,002127 kg /
kg AS
Or à l’état e2
de saturation, on a : x2
= x1 = cte ,
d’où
j1
= 1 et
x2 = 0,622
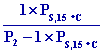
donc
P2
= PS,15°C +
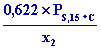= PS,15°C
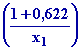car x2
= x1
On obtient
P2
= 17,04
=
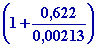5000 m bar @
4993
m bar
et
par conséquent
DP = P2
– P1 = 4,993 – 1 = 3,993 m bar
@
4 bar
2-
On
a x3L =
x3 -
x3S ( x3L est
la masse d’eau liquide )
or
x3 est
donnée d’après a-)
on a x1
= x3
on écrit
DP’ =
1,25 DP ( à la
Saturation )
P3-P1
= 1,25(P2-P1) =1,25 ´4 = 5 bar
, On obtient : P3
= 5 + P1 =
6 bar ,
xS,3
= 0,622
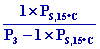= 0,622
=
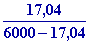0,00177 kg/kg AS
D’où la masse du liquide par kg d’air
sec :
x3L =
x3 - x3,S = 2,13 10-3 – 1,77 10-3
kg = 0,36 10-3 kg/kgAS
= 0,36 g/kg AS
x3L
=
0,36 g/kg AS
| 
