THERMODYNAMIQUE

Exercice 3:  Formule de Clapeyron. Point triple de l’eau

        On se propose d’étudier les équilibres entre les phases solide, liquide et gazeuse de l’eau au voisinage du point triple qui correspond à une température t₀ = 0,01 °C.

 1- Donner l’équation de l’isotherme relative à 1 g d’eau pour la température de 0 °C, en admettant que la vapeur d’eau peut être assimilée à un gaz parfait, et sachant que la pression de vapeur saturante de la glace est, à 0 °C, de 4,60 mm de mercure. On exprimera les volumes en cm³ et les pressions en mm de mercure.

2- On admet que la courbe de sublimation et la courbe de fusion peuvent être assimilées à des droites entre 0 °C et la température du point triple.

Sachant que la chaleur de sublimation de la glace à 0 °C est égale à 684 cal/g, calculer la pression du point triple.

3- Calculer la chaleur de fusion de la glace à la température de 0 °C.

On donne :  u_S  = 1 cm³/g ,   u_L = 1,09 cm³/g  et V_molaire (de la vapeur d’eau) : = 22,4 litres.

Solution 3 :

1- L’équation  de l’isotherme est p v = cte. Le point

         p  =  4,6 mm Hg = 613,3 Pa  , v = v_v  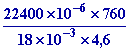=  = 205,603 m³

(car 760x0,022 = 1xRx273 et 4,6xV = (1/18) xRx273 et v = 205,603 m³)

 appartient à l’isotherme, donc :

                             p v = 126096 J

2- La chaleur de sublimation est donnée par la formule de Clapeyron , en négligeant le volume massique du solide par rapport à celui de la vapeur, on obtient :

           L_s = T v_V 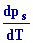   (  car  L_s = T( v_V - v_S ) 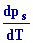  et v_S « v_V  )

     D’où     

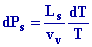
         donc 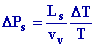 = = 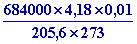0,51 Pa   =  0,004 mm Hg

et la pression du point triple :

                   P_T  =  4,60  +  0,004  =  4,604 mm Hg.

3- La chaleur de fusion est donnée par la formule de Clapeyron :

     L_F = 

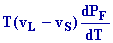
Avec   dP_F = DP_F =  760 – 4,604  =  755,396 mm Hg  ,   dT =  DT=  0,01 °K.

Par suite,  

    L_F = 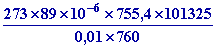=  349570 J/kg  = 83,63 cal/g