|
Série 5:
Changement de phase d'un corps pur
|
EXERCICE
1 :
On
considère 600 g d’eau
à la température t = 60 °C
qu’on mélange à 500 g
de glace à la température t2
= - 14 °C.
Si
la température d’équilibre tf
est
supposée nulle, déterminer les masses finales respectives d’eau
et de glace?
On
donne : Ce
= 1
cal / g °K ,
Cg
= 0,5 cal / g °K ,
Lf
= 80 cal / g
Solution
1 :
A la température tf = 0 °C ,quand
il y a changement de phase :
¨
ou bien on a fusion
d’une partie de la glace,
¨
ou bien on a solidification d’une
partie du liquide.
Dans
les deux cas on écrit ; Qp
= x L
avec :
·
x > 0 si le
changement d’état est une fusion.
·
x < 0 si le
changement d’état est une solidification.
Conclusion :
est la quantité de
glace ou de liquide qui s’est transformée.
On écrit : ( en tenant compte que tf
= 0 °C )
DU
= 0
= Qeau +
Qglace + x L
= 0
d’où meCe
( Tf -
T1 ) +
mgCg ( Tf - T2
) + x L
= 0
x = -
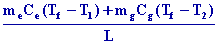
x
=
-
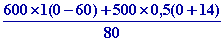= 406,25 g
Comme
x > 0 , donc il y
a 406,25
g de glace qui s’est transformée en eau ; on obtient :
·
600 + 406,25 g =
1006,25 g d’eau
·
500 – 406,25 =
93,75 g de glace
Exercice
2:
1-
a)1
litre
d’eau liquide est introduit dans une enceinte vide de 5
m3. La température est fixe et vaut 50
°C. En utilisant la formule de Duperray,
expliquer que se passe-t-il ?
b)En
admettant que la vapeur d’eau se comporte comme un gaz parfait,
combien y a-t-il d’eau
vaporisée à l’équilibre ?
2-
Dans un récipient clos de 5
m3 contenant de l’air sec à la pression 0,8
atm et à la température de 50
°C, on introduit 1
litre d’eau.
a)
Que
se passe-t-il en supposant que la température est maintenue
fixe?
b)
Quelles
sont à l’équilibre les valeurs de la pression partielle de
l’air, de l’eau vaporisée, et de la pression totale ?
quelle est la quantité d’eau vaporisée ?
Solution
1 :
1-
a
)
Pour calculer la pression de vapeur saturante de l’eau à t
= 50 °C, utilisons la formule de Duperray
PS = fS(T)
= P0
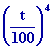( P0
= 1 atm et t en °C ) ;
On
trouve
PS =
0,062 atm = 6331
Pa.
L’eau introduite dans l’enceinte vide, va
se vaporiser jusqu’à ce que la pression de la vapeur atteigne la
valeur de la pression
de vapeur saturante.
b
) A
l’équilibre, on suppose que l’eau vaporisée occupe tout le
volume de l’enceinte, ( c’est à dire 5
m3 ) et que cette vapeur d’eau ( à PS
= 6331 Pa )
se comporte comme un gaz parfait ;
le
nombre de moles vaporisées est alors n
=
=
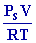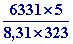= 11,8 moles
ce
qui correspond à m
= n M = 11,8 ´ 18 = 212 g d’eau.
2-
Dans un récipient clos de 5
m3, où la pression initiale d’air
est 0,8
atm à 50 °C, l’eau
introduite va s’évaporer jusqu’à ce que la pression partielle
de l’eau atteigne la pression de vapeur saturante ( calculée en 1-
a
).
A
l’équilibre, la pression partielle de l’air est 0,8 atm, la pression de l’eau vaporisée vaut 0,062 atm et la pression totale vaut 0,862 atm.
Pour
l’évaporation seule compte la pression partielle de vapeur ( qui
est la même que précédemment ) : la quantité d’eau
vaporisée sera donc la même, soit 212
g.
| 
