|
Série 4: Le
second principe de la thermodynamique : Les cycles
|
EXERCICE
1:
Cycle
de Beau de Rochas ou Otto
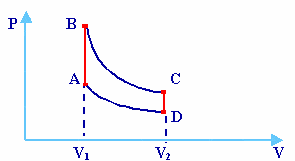
Pour faire fonctionner une moissonneuse-batteuse, on utilise n
moles d’un gaz parfait qui décrivent le cycle de Beau de Rochas
dans le sens indiqué sur la figure. Les transformations DA
et
BC sont
des adiabatiques alors que les transformations CD
et
AB sont
des isochores. On désigne par
a
=V2
/ V1 le
rapport des volumes (taux de compression). Cv
est
supposé constant pendant tout le cycle.
1–
Exprimer
la quantité de chaleur reçue par le gaz pendant l’explosion AB
en
fonction de TA
et
TB
.
2–
Déterminer
le travail W
fourni
pendant le cycle en fonction des températures.
3–
En
déduire le rendement du cycle en fonction des températures.
4–
Montrer
que ce rendement s’exprime simplement en fonction de
a
et
de g
5–
Donner
l’expression de la variation d’entropie au cours des différentes
transformations
Application
numérique :
a
=
9 ; g
=
1,4.
Solution
1 :
1- S’il y a n moles de gaz parfait dans le cylindre on a :
QAB = n CV
( TB -
TA
)
QAB est
positif
2- WAB
= WCD
= 0 puisque
AB et CD sont isochores.
WBC = DUBC = n CV
( TC -
TB )
puisque BC est
adiabatique.
WDA = DUDA
= n CV
( TA -
TD )
puisque DA est
adiabatique.
W = WBC
+ WDA
= n CV ( TC
- TB
+ TA
- TD
) négatif.
3- h
=
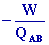 =
=
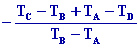 =
=
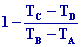
4-
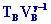 =
=
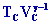 et
et
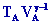 =
=
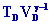
D’où
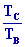 =
=
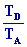 =
=
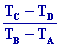 =
a( 1 - g)
et h
= 1 - a( 1 - g)
=
0,585 =
a( 1 - g)
et h
= 1 - a( 1 - g)
=
0,585
DSAB = n CV ln
 ; DSBC = 0 ;
DSCD
= n CV
ln
; DSBC = 0 ;
DSCD
= n CV
ln
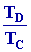 et
DSDA
= 0
et
DSDA
= 0
EXERCICE
2:
Une centrale thermique électrique, qu’elle soit alimentée
en combustible nucléaire ou fossile, est une machine thermique qui
fonctionne selon le cycle de Carnot entre la température du réacteur
(ou du foyer) et celle du milieu ambiant représenté en général
par un fleuve (ou une autre masse d’eau). On considère une
centrale nucléaire moderne de 750000
KW ; la température du réacteur atteint 315
°C et on dispose d’un fleuve à 21
°C.
1–
Quel rendement thermique maximal peut-on obtenir de la
centrale et quelle quantité minimale de chaleur doit être rejetée
dans le fleuve ?
2
–
Si
le rendement théorique effectif de la centrale est 60 % du
rendement théorique maximal, quelle quantité de chaleur doit être
rejetée dans le fleuve et quelle sera l’augmentation de la température
de ce dernier si son débit est 165
m3 / s ?
Solution
2 :
Cycle de Carnot Þ
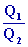 =
=
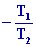 voir le cours
voir le cours
1-
Le rendement r =
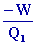 = 1
-
= 1
-
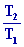 =
1 -
=
1 -
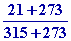 = 0,5
= 0,5
Dans ce cas
50 %
de chaleur sont convertis en travail et 50
%
de chaleur sont rejetés dans le fleuve,
or W
= 750 000 kW =
760 106 J / s et
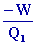 = 0,5 avec DU
= W + Q1 + Q2
= 0
= 0,5 avec DU
= W + Q1 + Q2
= 0
D’où
Q2
= 750 000 KW
= 750 106
J / s
2-
Si le rendement réel h
= 60 %
de la valeur théorique, on a h = 0,6r
= 0,6 ´
0,5 =
0,30
or
h =
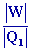 Þ
Þ
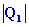 =
=
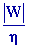 =
=
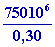 =
2,5 109 J / s
=
2,5 109 J / s
Les 70
%
de cette quantité qui ne sont pas convertis en travail, sont rejetés
dans le fleuve , donc :
Q2 =
0,7 ( 2,5 10 9 )
= 1,75 109
J / s = 1750 000 KW
On a le débit 165
m3 / s =
165 103 kg / s
; puisque Q2 =
m C DT
DT
=
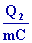 =
=
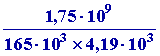 =
2 ,54 °K
=
2 ,54 °K
Cette élévation de température provoquée
par une centrale thermique est appelée aussi pollution
thermique.
|