|
Série
3 (suite):
Le
second principe de la thermodynamique
|
EXERCICE
3:
On considère un cylindre horizontal de volume invariable qui
est divisé en deux compartiments A
et B
par
un piston mobile se déplaçant sans frottements. On suppose que les
deux
compartiments
et le piston sont athermanes et qu’à l’instant initial les deux
compartiments A
et B
ont
le même volume V0 =
2 l
d’hélium
(gaz parfait), à la pression
P0
= 1 atm,
et
à la température T0 =
273 °K , g
= 5 / 3 ;
le gaz du compartiment C1
reçoit à l’aide d’une résistance chauffante, de la
chaleur du milieu extérieur.
Déterminer :
1-
Les pressions, les volumes et les températures des compartiments
C1 et C2,
lorsque la pression du gaz contenu dans C1
devient P1 =
3P0
2-
La variation d’énergie interne du gaz dans C1
et C2 et
l’énergie fournie par la résistance chauffante.
Solution
3 :
1- L’équilibre mécanique se
traduit par P1 = P2
= 3P0 = 3 atm
dans le
compartiment C2 le
gaz a subi une transformation
adiabatique donc :
P0
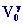= P2
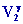Þ V2 = V0
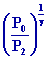
donc
V2 = 1,03
l
et V1
= 2 V0 - V2 = 2,97 l
Pour T2
= T0
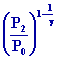Þ T2 = 423,7 °K
Pour T1
on utilise P V = n R T Þ T1 = T0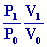 
= 1216 °K
2- DU1 = n CV
( T1 – T0 ) or
CV
=
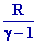
DU1 =
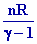( T1 – T0 ) =
=
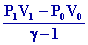1040 KJ
De
même DU2 =
=
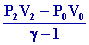164 KJ
La résistance
électrique a fourni l’énergie : E =
DU1 + DU2 =
1204 KJ
EXERCICE
4:
On considère un cylindre fermé, dont les parois sont
adiabatiques. Les deux compartiments
A et B,
séparés
par un piston qui est fixe au départ, contiennent de l’air. Dans A
l’air
est dans l’état ( P0,V0,T0
)
et
dans B, il est dans l’état
( 2P0,V0,T0
).
On
considère le piston mobile, lorsque l’équilibre est établi, détermine
la pression finale P1
de
l’air, ainsi que les volumes et les températures du gaz, dans
chaque compartiment. On admettra que le déplacement du piston
s’effectue de façon quasi-statique.
A.N :
P0 = 1 atm
; g
= 7 / 5 ;
V0 = 2 l ;
T0 = 300 °K.
| 
