|
Série 3: Le
second principe de la thermodynamique
|
EXERCICE 1:
Une personne respire 12 l d’air par minute à la température de 20 °C et le rejette à 45 °C. En considérant que l’air est un gaz parfait diatomique de masse molaire M = 29 g/mole ; calculer la quantité de chaleur fournie pour le réchauffement de l’air respiré en 24 heures. On suppose que la composition de l’air reste inchangée entre l’inspiration et l’expiration sous une pression constante d’une atmosphère.
On donne : la masse volumique de l’air
r
= 1,24 Kg.m-3 ;
la constante des gaz parfaits R = 8,32 S.I.
Solution 1:
La masse d’air réchauffée en 24 h est :
m = r
V n24
avec r : masse volumique , V : volume d’air,
n24 : nombre de minutes en 24 h
d'où m = 1,24x 12 10 –3
x60x 24 = 21,427 kg
Le nombre de moles d’air est : n = 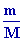 =
= 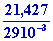 =
738,86 moles. =
738,86 moles.
La quantité de chaleur fournie pour le réchauffement de l’air respiré en 24 h est :
Qp = n Cp DT
avec Cp = 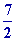 R gaz diatomique R gaz diatomique
Qp = 738,86
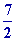 8,32 x ( 45 – 20 ) = 537,882 KJ
8,32 x ( 45 – 20 ) = 537,882 KJ  538 KJ 538 KJ
Remarque :on utilise Cp car la pression est supposée constante, alors que le volume varie au cours de la transformation.
EXERCICE
2:
a- Calculer la pression atmosphérique à l’altitude z ; sachant que les conditions atmosphériques au sol sont caractérisées par la température
T0 et la pression P0 et que la température varie avec l’altitude selon la loi : T =
T0 – k z .
b- Déterminer la relation liant l’altitude z à la pression P au cours de l’ascension d’une masse d’air (en le supposant comme gaz parfait) qui s’élève dans l’atmosphère sans échange de chaleur avec l’extérieur (d’une façon adiabatique).
On donne : z = 4000 m ; P0 = 750 mm Hg ; T0 = 293 °K; g = 10 m
s-2
k = 0,005 °K /m ; r0
= 1,19 Kg.m-3 ; g
= CP
/Cv
= 1,4
Solution
2:
1- La différence de pression entre deux points d’altitude z et z + dz est donnée par l’équation de l’hydrostatique : dP = -
r
g dz où la masse volumique r de l’air ( gaz supposé parfait) est : r =
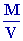 avec PV = RT , soit
r
= avec PV = RT , soit
r
= 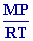
on en déduit dP = - P 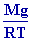 dz , soit dz , soit
 = - = -
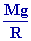 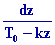
Intégrons entre l’altitude O et l’altitude z ; il vient : Ln 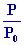 = = 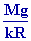 Ln Ln
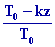
La relation pression - altitude s’écrit donc : P(z) =
P0 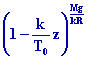
2-
Relation ( T, P )
Lorsque la masse d’air passe de l’altitude z à l’altitude voisine z + dz, sa pression passe de P à P + dP et sa température de T à T + dT de façon à satisfaire la loi adiabatique
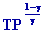 = cte que l’on écrit sous la forme différentielle : = cte que l’on écrit sous la forme différentielle :
 + +
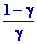  = 0
¬ = 0
¬
· Relation ( P, z )
L’équation fondamentale de l’hydrostatique s’écrit :
dP = - r
g dz avec PV = RT pour une mole d’air,
donc : r
= 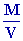 = =
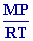 ,
soit dP = - ,
soit dP = -
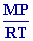 g dz ou g dz ou
 + +
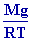 dz = 0
® dz = 0
®
· Relation ( T, z )
Éliminons la pression P entre ¬
et ®, il vient : dT +
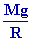 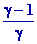 dz = 0 dz = 0
On en déduit le gradient vertical de température, correspondant à l’équilibre adiabatique de l’atmosphère
Ka = 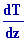 = - = -
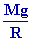 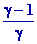 ¯ on pose
Ka = - ¯ on pose
Ka = -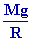 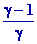 =cte =cte
A.N
Ka = - 9,76 10-3 k / m
Le gradient thermique Ka est constant, si on suppose g
et g constants,
on obtient donc en intégrant ¯ T =
Ka z + T0 ,
soit T = T0
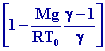 °
et P = P0 °
et P = P0 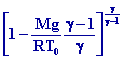 ±
car ±
car 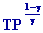 = cte = cte
La masse volumique de l’air à l’altitude z est d’après ,
°
et ± :
r =
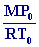
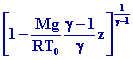
|