|
Série
2 :
Le
premier principe de la thermodynamique
|
EXERCICE
1 :
En
hiver et afin d’éviter le gel, on chauffe une serre contenant 812
g d’air (gaz supposé parfait) dont la température s’élève
de 2° C
à 16° C.
Calculer :
a
-
la variation d’énergie interne de l’air au cours de cet
échauffement ?
b
-
la quantité de chaleur reçue par le gaz, si ce dernier a
fourni un travail de 846,4
joules.
On
donne: La masse molaire
de l’air M
= 29 g /mole, R = 8,32 S.I. ;
Le rapport des chaleurs massiques de l’air
g
= CP /Cv =
1,4
Solution
1 :
a
- La
variation d’énergie interne de n
moles de gaz parfait :
DU
= n CV DT
L’air
est un gaz parfait diatomique : CV
=
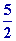R donc
:
DU =
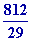
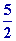
8,32
14 =
8153,6 J
b
-
On
a : DU
= W + Q ou
DU =
DW + DQ
La quantité de chaleur échangée par le gaz (l’air) est :
Q
= DU -
W
Or
W = - 846,4
car l’air a fourni un travail,
d’où Q = 8153,6
- ( - 846,4 ) = 9000
J
EXERCICE
2
:
L’état
initial d’une mole de gaz parfait est caractérisé par P0
= 2.105 Pascals,
V0
= 14
litres.
On
fait subir successivement à ce gaz:
- une détente
isobare, qui double son volume,
-
une compression isotherme, qui le ramène à son volume
initial,
-
un refroidissement isochore, qui le ramène à l’état
initial (P0
,
V0 ).
a
- A
quelle température s’effectue la compression isotherme ? En déduire
la pression maximale
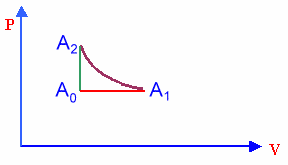
atteinte. Représenter le cycle de transformation dans le diagramme
(P,
V )
b
- Calculer
le travail, la quantité de chaleur et la variation d’énergie
interne échangés par le
système au cours de chaque transformation ?. Faire le
bilan du cycle ?.
On donne : constante des gaz parfaits : R
= 8,314 J.K-1.
Solution
2 :
a
- L’état
initial du gaz, représenté par le point A0,
est caractérisé par :
P0 =
2 105 Pa
; V0
= 14 10-3
m3
; T0
=
=
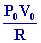336,78 °K
n A la
fin de la détente isobare, l’état du gaz, représenté par le
point A1, est caractérisé par :
P1 = P0 ;
V1 = 2 V0
; T1
=
=
=
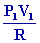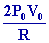2 T0 =
673,56 °K
n
A la fin de la compression isotherme, l’état du gaz représenté
par le point A2,
est caractérisé par
P2
=
=
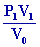2 P0
( d ‘après la loi de Mariotte ) ;
V0 ;
2 T0
La pression
maximale du gaz est donc :
P2 = 2 P0
= 4 105 Pa
b
-
u Au
cours de la détente isobare
A0A1 on a :
W1
= - P0
( 2 V0 -
V0 ) = - P0
V0 =
- 2800 J
Q1
= CP
( T1 -
T0 ) =
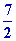8,314
336,78 = 9800 J
u Au
cours de la compression isotherme A1A2
on a :
W2 = R T1 ln
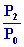= 2 R T0 ln 2 = 3881,61
J
Q2
=
=
R T1 ln
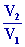= - 2 R T0 ln 2
= - 3881,61 J
u Au
cours du refroidissement isochore
A2A0 on a :
W3 = 0 J (
à volume constant)
Q3
= CV
( T0 -
T1 ) = -
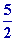8,314
336,78 = -7000 J
| Transformation |
W en J |
Q en J |
DU= W+Q
en J
|
| Isobare
|
-2800
|
9800
|
7000
|
| Isotherme
|
3881,61
|
-3881,61
|
0
|
| Isochore
|
0
|
-7000
|
-7000
|
|
total
|
1081,61 |
-
1081,61
|
0
|
Au cours du
cycle :
Le bilan mécanique du cycle est donc :
W
= W1 + W2 + W3 =1081,61 J /mole.
La quantité de chaleur échangée est donc :
Q
= - W = - 1081,61
J / mole
La
variation de l’énergie interne est
nulle car c’est une fonction d’état.
W est positif, Q est négatif ; par conséquent, le système a reçu un
travail qu’il a intégralement restitué au milieu extérieur sous
forme de chaleur.
| 
