THERMODYNAMIQUE

1. ÉNERGIE LIBRE  F , ENTHALPIE  LIBRE  G

                  1.1.  Définitions

On définit à partir des fonctions d’état énergie interne U et enthalpie H d’un système et des variables conjuguées T et S, les nouvelles fonctions d’état suivantes :

Énergie libre :

                                    F = U - TS

Enthalpie libre :

                              G = H - TS

               1.2.  Différentielles

Pour un système fermé fluide soumis uniquement aux forces de pression :

 dF = - SdT –  pdV

dG = - SdT + Vdp

Pour un système fermé pour lequel dW = 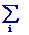Y_i dX_i représente la somme des travaux, on généralise les définitions de l’énergie libre et de l’enthalpie libre en écrivant les différentielles sous la           forme :

                        dF = - SdT + 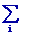  Y_i dX_i

                        dG = - SdT – 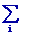  X_i dY_i

Pour un fil élastique de longueur L soumis à une forme de traction Á :

                        dF = - SdT + Á dL

                       dG = - SdT – LdÁ

Pour un diélectrique de permittivité relative e_r (p, T) placé dans un condensateur de charge q sous la différence de potentiel U :

                      dF =  -  SdT –  pdV + Udq

                      dG = -  SdT +  Vdp – qdU

2.INTERPRETATION  PHYSIQUE

Lors d’une transformation monotherme d’un système avec une source de température T₀ on peut écrire :

                   DF =  DU – T₀  DS  = W + Q – T₀ DS

                   DG = DH – T₀  DS = W + Q + D(pV) - T₀ DS

                   DS = (Q/  T₀) + S^p ³ Q/ T₀

       2.1 Pour l’énergie libre

On en déduit pour une telle transformation :

DF  £ W

La variation d’énergie libre est donc inférieure, ou dans le cas réversible égale, au travail échangé.

Si dans une transformation monotherme le système fournit du travail au milieu extérieur, ce travail est au plus égal à la diminution d’énergie libre du système d’où la dénomination de cette fonction.

Si de plus le système soumis uniquement aux forces de pression subit une transformation isochore : DF £ 0

Les transformations spontanées monothermes d’un système soumis aux seules forces de pression entraînent une diminution de F pour les transformations isochores : DF  £ 0

       2.2 Pour l’enthalpie libre

On en déduit pour une telle transformation :

DG  £ W  +   D (pV)

Cette relation prend une forme particulièrement simple si la transformation est de plus monobare car W +  D (pV) = 0 et on a donc : DG £  0.

Les transformations spontanées monothermes d’un système soumis aux seules forces de pression entraînent une diminution de G pour  les transformations monobares : DG £  0.

Tout système évoluant dans l’une ou l’autre de ces conditions pourra aboutir à un état d’équilibre où sa fonction F ou G sera donc minimale.

Ces fonctions qui jouent un rôle analogue à celui de l’énergie potentielle en mécanique sont pour cette raison appelées potentiels thermodynamiques.

3. PROPRIÉTÉS DES DIFFÉRENTIELLES

          3.1 Relations de Maxwell

Pour un système soumis aux seules forces de pression, en écrivant que dU, dH, dF et dG sont des différentielles totales, on obtient en particulier les relations suivantes :

                        S =  -

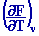
                        S =  - 

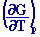
         3.2 Relations de Gibbs-Helmholtz

En éliminant l’entropie S des expressions de F et G, on trouve :

                      U = F – T

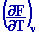
                      H = G – T
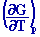