|
Chapitre
6:
APPLICATIONS DES DEUX PRINCIPES A UN SYSTÈME HOMOGÈNE
|
1-
ÉTUDE D’UN FLUIDE HOMOGÈNE :
1.1 Expressions provenant des deux principes de la thermodynamique:
on utilise les relations suivantes pour une transformation élémentaire quasi statique relative à l’unité de masse d’un système fermé monophasé défini par sa pression p, son volume massique v et sa température T : système ( p, v,
T).
pour tout système (p, v, T) :
du = T ds - p dv
dh = T ds + v dp
et dans le cas de la réversibilité :
ds = dqrev / T
T ds = cv dT + l dv
T ds = cp dT + h dp
T ds = l dT + m dv
On en déduit des expressions de la forme :
cv =
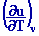 = T = T
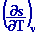
cp = 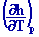 = T = T
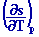
1-2 Les relations :
on écrit que ds et du sont des différentielles.
Première relation de Clapeyron :
l = T
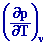
on écrit que ds et dh sont des différentielles :
deuxième relation de Clapeyron :
h = - T 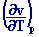
Relation de Mayer :
Cp – Cv = T 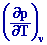 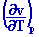
Lors des deux premiers calculs on obtient deux autres relations utiles :
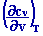 =
T
=
T
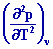
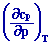 =
- T
=
- T
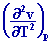
2. LE GAZ PARFAIT :
2.1 Équation d’état :
A la température T, sous la pression p, n moles d’un gaz parfait occupent un volume V tel que :
P V = n R T , R = 8.314 J/K/ mol : Constante des gaz parfaits
Autres formes de cette équation :
p v = r T
p = r
r T
v est le volume massique, r la masse volumique et r est le rapport de la constante des gaz parfaits et de la masse molaire du gaz : r = R/M.
Loi
de Boyle-Mariotte :
A température constante, le produit pV de la pression par le volume est constant.
Loi
d’Avogadro :
A la même température et sous la même pression, des volumes égaux de gaz parfaits contiennent le même nombre de moles.
En particulier à la température T0 = 273.15 °K sous la pression p = 1.013 105 Pa,
le volume molaire
Vm d’un gaz parfait vaut : Vm = 22.4 l/mol.
Loi
de Gay-Lussac :
A pression constante, le volume molaire Vm est proportionnel à la température T.
Loi
de Charles :
A volume constant, la pression d’une masse de gaz parfait est proportionnelle à la température T.
Loi
de Dalton :
La pression totale d’un mélange de gaz parfaits contenu dans un récipient de volume V à la température T est la somme des pressions partielles, c'est-à-dire la somme des pressions qu’aurait chaque gaz s’il occupait seul le même volume à la même température.
2.2. Les coefficients thermoélastiques
| Fluide
quelconque
|
Gaz
parfait
|
|
a
= (1 / V)
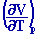
|
a
= 1/ T
|
|
b
= (1/ p)
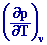
|
b
= 1/ T
|
cT
= (-1/ V)
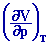
|
cT
= 1/ P
|
cS
= (-1/ V)
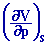
|
cS
= 1/ gP
|
2.3.
Les coefficients calorimétriques :
2.4
Les fonctions u, h et s
| Fluide
quelconque
|
Gaz
parfait
|
|
du
= cv
(T, v) dT + (l – p) dv
|
du
= cv (T) dT
|
|
dh
= cp (T, p) dT + (h + v) dp
|
dh
= cp (T) dT
|
|
ds
= cp (T, p) dT / T + h dp/ T
= cv
(T, v) dT/ T +
l dv/ T
|
ds
= cp (T) dT / T - r dp/ p
= cv (T) dT/
T + r dv/ v
|
Première
loi de Joule
L’énergie interne d’un Gaz parfait ne dépend que de la température.
Si cv constant
D
U = m cv
DT
Lors d’une détente de Joule, détente isoénergétique, les températures initiale et finale d’un gaz parfait sont
identiques. Pour un gaz réel aux températures usuelles, on observe un léger refroidissement, sauf pour l’hélium.
Deuxième
loi de Joule :
L’enthalpie d’un gaz parfait ne dépend que de la température.
Si cp constant;
DH = m
cp
DT
Lors d’une détente de Joule Thomson, détente isenthalpique, les températures initiale et finale d’un gaz parfait sont
identiques. Pour un gaz réel aux températures usuelles, on observe un léger refroidissement, sauf pour l’hélium et l’hydrogène.
Variante
d’entropie d’un gaz parfait avec cp (ou cv)
constant :
DS = m cp ln (T2/ T1) – n R ln
(P2 / P1) = m cv ln (T2/
T1 ) + n R ln (V2 / V1)
On en déduit la loi de laplace relative à la transformation adiabatique réversible d’un gaz parfait :
pVg
= cte
Ou
sous d’autres formes :
P1 – g
Tg
= cte ou
T V g
- 1 = cte
2.5 Les transformations
Transformation
monotherme de n moles d’un gaz parfait de l’état initial (P1,
V1, T0) à l’état final (P2, V2,
T0).
| |
Transformation monotherme
d’un gaz parfait |
Transformation irréversible
(On suppose la pression extérieure Pext constante)
|
P1 V1 =
P2 V2
DU = 0 et
DH = 0
W = -Q = - pext (V2 – V1)
DS
= n R ln V2 / V1
Se = Q / T
Sp = n R ln V2/V1-Q/ T0 > 0 |
Transformation irréversible :
transformation isotherme
|
PV = cte
DU = 0 et
DH = 0
W = -Q = - pext (V2 – V1)
W = -Q = - 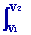 pdV pdV
= - nRT0 ln V2/V1
DS = n R ln
V2/ V1
Se = Q / T0 = DS et Sp = 0 |
Transformation adiabatique de n moles d’un gaz parfait de l’état initial
(P1, V1, T1) à l’état final (P2,
V2, T2) en supposant la capacité calorifique massique
cp constante.
| |
Transformation adiabatique
d’un gaz parfait ( g
est supposé constant) |
Transformation irréversible
(On suppose la pression extérieure Pext constante) |
(P1 V1 ) /
T1 = (P2 V2) / T2
Q = 0
DU = W = m
cv ( T2 – T1)
W = - pext (V2 –
V1)
DS = m
cp ln (T2/ T1 ) – n R ln
P2/P1
Se = 0
Sp = DS > 0 |
Transformation réversible :
transformation isentropique |
PVg
= cte
Q = 0
DU = W = m cv
(T2 – T1)
W = - 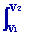 pdV = (1/
g
- 1) (p2 V2 - p1V1) pdV = (1/
g
- 1) (p2 V2 - p1V1)
DS = 0
Se = 0
Sp = 0 |
|