THERMODYNAMIQUE

1. LE SECOND PRINCIPE : PRINCIPE D’ÉVOLUTION

                1.1. L’entropie S

Pour tout système, il existe une fonction d’état extensive l’entropie S, non conservative.

                1.2. Bilan entropique

La variation d’entropie  DS d’un système fermé entre deux instants successifs t₁ et t₂ s’écrit :

                                   DS = 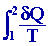    + S^p  avec  S^p ³  0

Sous forme différentielle :

                                   dS =   +  d S^p

Où :     dS représente la différentielle totale exacte de la fonction d’état ;

           dQ et  dS^p représentent des formes différentielles ;

            T est la température thermodynamique définie en chaque point de la surface et

               correspond à la température absolue.

Le premier terme 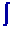  dQ / T correspond à l’entropie échangée S^e

Le second terme S^p correspond à l’entropie produite et le système est alors le siège de phénomènes irréversibles provenant :

-         de transferts de chaleur, de masse, provoqués par des hétérogénéités, de température, de concentrations ;

-         de frottements mécaniques, de viscosité ;

-         de réaction chimiques, d’hystérésis.

• Si S^p > 0 la transformation est irréversible.

• Si S^p = 0 la transformation est réversible.

L’unité d’entropie est le joule par Kelvin : J/K

2. CONSÉQUENCES

         2.1. Différentes formulations

• L’entropie d’un système isolé  ne peut que croître ou rester constante :

                                 DS = S^p   ³ 0

• Pour un cycle :

                                 DS = 0

• Pour une transformation réversible :

                                 dS =   dQ _rev /  T

• Une transformation adiabatique réversible est une transformation isentropique :

                                 dS = 0

Une transformation isentropique n’est pas toujours adiabatique réversible :

                              dQ /  T + dS^p = 0

                    2.2. Autres formulations du second principe

• Énoncé de Clausius : La chaleur ne passe pas spontanément d’un corps froid à un corps chaud.

• Énoncé de Kelvin : Un système décrivant un cycle monotherme ne peut que recevoir du travail et fournir de la chaleur.

                  2.3. État d’équilibre et réversible

Le second principe permet de préciser la définition de l’état d’équilibre d’un système :

Un système homogène se trouve dans un état d’équilibre par rapport à un repère :

-         s’il est immobile : sa vitesse d’ensemble par rapport au repère est nulle ;

  -         si les variables d’état ne varient pas au cours du temps : état stationnaire ;

Les variables intensives ont alors la même valeur en tout point du système en l’absence de champ de forces extérieures.

Une transformation est réversible si la création d'entropie S^p est nulle

                  2.4. Identité thermodynamique

On étudie souvent une masse de fluide globalement immobile et soumise  uniquement à des forces de pression. Pour une transformation réversible :

                     dQ = T dS   donc  dU = T dS – p dV

Les grandeurs qui interviennent dans cette équation sont des fonctions ou des variables d’état :

Lors d’une quelconque transformation infinitésimale d’un système fermé soumis aux seules forces de pression :

                      dU = T dS – p dV

On en déduit que U est une fonction de S et V et que S est une fonction de U et V

                       dS =     (dU / T )  + ( P / T)

Les variables T et S forment un couple de variables conjuguées.

   3. EXEMPLES DE BILAN

S étant une fonction d’état, la variation d’entropie au cours d’une transformation irréversible entre deux états d’équilibre peut être calculée en utilisant le chemin entre ces deux états :

                       DS  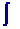 =   dQ _rev  / T =  S^e +  S^p

Les calculs de l’entropie échangée S^e puis de l’entropie produite S^p  peuvent être réalisés :

- si la transformation est réversible       :    DS = S^e et S^p est nulle ;

- si la transformation est adiabatique     :   S^e est nulle et   DS = S^p ;

- si le système est en contact avec une source de chaleur qui fixe la température de la surface du système à T_S pendant la transformation et donne au système la chaleur Q :

                          S^e  =  Q / T_S et  S^p  =  DS – S^e.