THERMODYNAMIQUE

1. LE PREMIER PRINCIPE : CONSERVATION DE L’ÉNERGIE
 

       1.1 Énergie interne U, énergie totale E
Pour tout système, il existe une fonction d’état appelée énergie interne U, telle que l’énergie totale E, fonction extensive, somme de l’énergie cinétique macroscopique Ec, de l’énergie potentielle extérieur Ep et de l’énergie interne U soit conservative :

                               E = E_c + E_p + U

E_c est l’énergie cinétique macroscopique due au mouvement d’ensemble du système dans le repère d’étude.

E_p est l’énergie potentielle provenant des forces extérieures : forces électromagnétiques, forces de pesanteur.

L’énergie interne U s’interprète comme la somme de l’énergie cinétique microscopique E_{c, micro} des particules du système et de leur énergie potentielle d’interaction E_p,int.

                                 U =  E_{c, micro} + E_p,int.

         1.2 Bilan énergétique
La variation d’énergie totale d’un système fermé se réduit à l’énergie échangée à travers la surface avec le milieu extérieur sous forme :

      -         de travail W des forces extérieures appliquées en chaque point de la surface ;

-         de chaleur Q.

                       DE =  DEc + DEp + DU = W + Q

sous forme différentielle, cela donne :

                     dE + dEc + dEp + dU =  d W + dQ

où : dE représente la différentielle totale exacte de la fonction d’état ;  dW et  dQ représentent  des formes différentielles.

 La variation d’énergie totale DE ne dépend que de l’état final et de l’état initial de la transformation et non du chemin suivi contrairement aux quantités  W et Q.

      2. CONSÉQUENCES
           

L’énergie totale d’un système isolé se conserve.

                dE = O

 Pour un cycle :

                DE = W + Q = O

 Ce résultat est appelé “principe de l’équivalence”.

Pour un système fermé, non soumis à des forces extérieures dérivant d’un potentiel, le bilan d’énergie prend la forme :

                DEc + DU = W + Q

 Pour un système fermé en l’absence de variation d’énergie cinétique macroscopique et non soumis à des forces extérieures dérivant d’un potentiel, le bilan d’énergie prend la forme de l’expression bien connue :

                DU = W + Q

 Sous forme différentielle, cela donne :

                dU =  dW + dQ

La fonction énergie interne est alors une grandeur extensive conservative.

          3. TRAVAIL

                  3.1. Travail élémentaire des forces extérieures

Le travail élémentaire des forces extérieures de contact sur un élément de surface du système lors du déplacement de cet élément s’écrit :

dW =  .

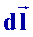
 Le travail des forces de pression représente un cas particulier important.

                 3.2. Travail élémentaire des forces extérieures de pression

 Le travail des forces de pression extérieures lors du déplacement élémentaires d’un élément de paroi de surface dS est :

dW =  - p_ext .dV

Où dV représente la variation de volume du système.

Lors d’une transformation isochore, le système est mécaniquement isolé.

              3.3. Travail élémentaire des forces extérieures de pression lors d’une transformation quasi statique.

Lors d’une transformation quasi statique, la pression p du système est égale à la pression extérieure p_ext :

                                      dW = - p dV

Le bilan énergétique s’écrit alors, pour un système fermé soumis aux seules forces de pression,

                                       dU =  dQ - pdV

              3.4. Autres expressions du travail élémentaire

Des systèmes différents décrits par d’autres variables peuvent être considérés (cf. tableau ci-dessous).

On remarque l’analogie entre les expressions de ces différents travaux : le travail élémentaire apparaît toujours comme le produit d’une variable intensive Y_i , par la variation élémentaire d’une variable extensive X_i. Ces deux variables sont dites conjuguées.

 Le travail élémentaire total accompli sur un système s’exprime alors par :

                               dW   =  

Le travail dépend du chemin suivi. L’unité de travail est le joule (J).

       4. CHALEUR

Les échanges d’énergie non réductibles à un travail s’appellent chaleur.

 Ce transfert d’énergie se fait sous la forme d’énergie cinétique moléculaire correspondant à une agitation désordonnée.

La chaleur dépend du chemin suivi. L’unité de chaleur est le joule (J).

Les transferts d’énergie sous forme de chaleur se font :

-         par conduction dans les fluides et les solides

-         par convection dans les fluides ;

-         par rayonnement.

Dans le vide, seul le rayonnement intervient.

Ces transferts existent entre deux corps à températures différentes mis en contact mais aussi entre une source de chaleur et un corps subissant un changement d’état à température constante.

 Pour un système soumis aux seules forces de pression dans une transformation quasi-statique isochore, la chaleur s’identifie avec la variation d’énergie interne :

DU =  Q_v

      5. L’ENTHALPIE   H

On définit une fonction d’état H à partir de l’énergie interne U, de la pression p et du volume V :

                    H = U + pV

 Sous forme  différentielle :

                  dH = dU + pdV + Vdp

L’unité d’enthalpie est le joule (J).

Pour un système fermé soumis aux seules forces de pression dans une transformation élémentaire quasi statique :

                   dH =  dQ + Vdp

Pour un tel système, la chaleur s’identifie avec la variation d’enthalpie dans une transformation quasi statique isobare :

                   DH = Q_p

Exercices:

Calculer le travail effectué par 10 moles de gaz parfait, lorsqu'on les soumet à une dilatation de 1 atm à 0ºC jusqu'à 0.1 atm à 0ºC selon chacun des chemins suivants:

a)

on diminue la pression extérieure jusqu'à la pression finale en maintenant le volume constant, puis on laisse le gaz se dilater à pression constante jusqu'au volume final;

b)

on diminue la pression extérieure jusqu'à une pression de 0.5 atm en maintenant le volume constant, puis on laisse le gaz se dilater à pression constante, ensuite on diminue à nouveau la pression à volume constant jusqu'à la pression finale et on laisse enfin le gaz se dilater à pression constante;

c)

à température constante T = 0ºC, en maintenant la pression extérieure égale à chaque instant à la pression du gaz. Dans ce cas, le processus est conduit par une succession de variation infiniment petites par rapport à l'état d'équilibre du système. Le processus peut donc à tout instant être renversé. Le processus (c) est réversible.

 Réponses: a) wa=-20438 J; b) wb=-29522 J; c) wc=-52291 J

Calculer le travail effectué lorsque l'on vaporise une mole d'eau liquide à 100ºC sous pression atmosphérique constante. Les volumes spécifiques du liquide et de la vapeur à 100ºC sont respectivement 1 et 1720 cm3.g-1.