|
Chapitre
1:
GENERALITES SUR LES
SYSTÈMES THERMODYNAMIQUES
|
1. DESCRIPTION
D'UN SYSTÈME
1.1 Système et milieu extérieur
Un système est une partie de l'univers limitée par une surface fermée et comprenant un grand nombre de particules.
Cette surface peut être fictive ou matérielle.
Le milieu extérieur est la partie de l'univers qui n'appartient pas au système.
1.2 Système isolé, ouvert, fermé
Le système et le milieu extérieur peuvent échanger :
- De la matière,
- De l'énergie sous forme de travail ou de chaleur.
Un système isolé ne peut échanger ni énergie, ni matière avec le milieu extérieur.
Un système ouvert peut échanger de l'énergie et de la matière avec le milieu extérieur.
Un système fermé peut échanger de l'énergie mais pas de matière avec le milieu extérieur.
L'univers est un système isolé.
Les êtres vivants sont des systèmes ouverts.
Un système ouvert peut garder une masse constante.
Le gaz contenu dans un cylindre fermé par un piston est un système fermé.
1.3 Conventions de signe
Tout ce qui est reçu par le système est compté positivement.
Tout ce qui est cédé par le système est compté négativement.
1.4 Phase d'un système
Toute partie homogène d'un système constitue une phase
Un système monophasé ne comporte qu'une phase.
Un mélange de gaz constitue un système monophasé.
Un système polyphasé comporte plusieurs phases et constitue un système hétérogène.
Un gaz contenant de la fumée constitue un système polyphasé.
1.5 Variables d'état, équation d'état, fonctions d'état
1.5.1 Variables d'état :
Les variables d'état sont les variables qui définissent, à un instant donné, l'état macroscopique d'un système.
La masse, la quantité de matière, le volume, la pression, la température, la charge électrique, la concentration sont des variables d'état.
Le choix de ces variables est fonction du problème étudié.
1.5.2 Équations d'état
Certaines variables d'état peuvent être liées entre elles par une relation appelée équation d'état. Le système est alors définit par l'ensemble des variables d'état indépendantes.
Les exemples les plus connus sont :
·
l’équation d’état d’un gaz parfait
:
pV = n RT ;
·
l’équation de Van der Waals relative à n moles de
gaz
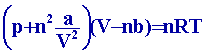
1.5.3 Fonctions d'état
Une fonction d'état est une fonction d'une ou plusieurs variables d'états indépendantes.
L'énergie, l'enthalpie, l'entropie sont des fonctions d'état.
Mathématiquement les fonctions d'état ont les mêmes propriétés que les variables d'état : le volume d'un gaz est une fonction de la pression et de la température.
1.6 Variables d'état extensives
1.6.1 Définition
Dans une phase, les variables d'état proportionnelles à la quantité de matière sont des variables extensives.
La masse, le volume, la charge électrique sont des variables d'état extensives.
Ce sont des grandeurs additives.
Une variable d'état extensive d'un système hétérogène est la somme des variables.
Une variable d'état extensive X se met sous la forme d'une intégrale de volume :
X (t) = 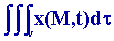
V est le volume du système et x (M, t) la densité volumique des la grandeur X au point M du système à l'instant t.
1.6.2 Bilan d'une grandeur extensive
La variation DX entre deux instants
t1 et t2 provient de deux contributions :
· Xe représente la quantité échangée par le système avec le milieu extérieur à travers la surface qui le délimite ;
· Xp représente la quantité produite dans le système
DX =
Xe + Xp
1.6.3 Grandeur extensive conservative
Une grandeur extensive est conservative si le terme de production est identiquement nul
Xp = 0
La masse en mécanique classique et la charge électrique sont des grandeurs conservatives.
La quantité de matière dans une réaction chimique est une grandeur non
conservative.
1.7. Variables d'état intensives
Dan une phase, les variables d'état qui ne sont pas proportionnelles à la quantité de matière sont des variables intensives.
La température, la pression, la masse volumique sont des variables d'état intensives. Dans le cas général, ces variables ont une valeur locale : on définit la pression en un point d'un fluide à un instant t.
1.8. Variance
Le nombre minimal de variables intensives que l'on doit connaître pour déterminer les autres variables intensives est appelé variance n du système.
Dans de nombreux cas, la variance n se calcule à partir du nombre c de constituant indépendants et du nombre de phases j du système grâce à la relation de Gibbs :
n = c + 2
– j
Un gaz est un système divariant.
2. ÉTATS D' ÉQUILIBRE
2.1.
États d'équilibre d'un système homogène
Un système homogène se trouve dans un état d'équilibre par rapport à un repère :
- s'il est immobile : sa vitesse d'ensemble par rapport au repère est nulle :
- si les variables d'état ne varient pas au cours du temps : état stationnaire :
- si les variables intensives sont la même valeur en tout point du système.
La dernière proposition n'est valable que si le système n'est soumis à aucune force extérieure à distance : force de pesanteur, forces électromagnétiques.
Si la température est la même en chaque point et n'évolue pas au cours du temps, on a un équilibre thermique.
Si la pression est la même en chaque point et n'évolue pas au cours du temps, on a un équilibre mécanique.
Ces deux équilibres ne s'établissent pas à la même vitesse : l'équilibre mécanique est en général plus rapidement atteint que l'équilibre thermique.
2.2 États d'équilibre d'un système hétérogène
Un système hétérogène constitué de plusieurs sous-systèmes homogènes est dans un état d'équilibre par rapport à un repère :
- si chaque sous-système est dans un état d'équilibre ;
- s'il n'existe aucun échange de matière et d'énergie entre les sous-systèmes.
Deux systèmes en équilibre thermique avec un même troisième sont en équilibre thermique entre eux. Ce principe zéro de la thermodynamique permet de caractériser la température des systèmes.
3. ÉVOLUTION D'UN SYSTÈME
Si un système est écarté de sa position d'équilibre initiale, les variables d'état changent du temps jusqu'à ce que le système parvienne à un nouvel état d'équilibre final : le système a subi une transformation.
3.1. Transformation adiabatique
La transformation d'un système est adiabatique si elle s'effectue sans échange de chaleur avec le milieu extérieur.
Le système est thermiquement isolé.
3.2. Transformation isotherme
La transformation d'un système est isotherme si elle s'effectue à température constante.
On ne confondra pas cette transformation avec une transformation monotherme où le système n'est en contact qu'avec une seule source de chaleur qui impose l'égalité des températures initiale et finale du système.
3.3. Transformation isobare
La transformation d'un système est isobare si elle s'effectue à pression constante.
3.4. Transformation isochore
La transformation d'un système est isochore si elle s'effectue à volume constant.
3.5. Transformation cyclique ou cycle
Une transformation est dite cyclique s'il y a retour à l'état initial à la fin de la transformation.
3.6. Transformation quasi statique
Il s'agit d'une transformation dont les accélérations restent toujours assez faibles pour que les lois relatives aux équilibres soient applicables.
Une transformation quasi statique est une suite continue d'états d'équilibre.
A tout instant de la transformation, les variables du système sont définies.
3.7. Transformation réversible
Une transformation est réversible si la transformation inverse passe par les mêmes états intermédiaires dans un ordre inverse.
Une transformation quasi statique n'est pas nécessairement réversible : la traction sur un fil en dehors de la limite d'élasticité peut être réalisée de façon quasi statique et est irréversible.
3.8. Transformation réelles
Toute transformation non réversible est irréversible. Les transformations réelles sont irréversibles.
Le système est alors le siège :
- de transfert de chaleur, de masse provoqués par des hétérogénéités de température, de concentrations ;
- de frottements mécaniques, de viscosité ;
- de réactions chimiques, d'hystérésis ;
- d'effet Joule.
4. UNITÉS
| Grandeur
|
Nom
|
Symbole
|
| masse |
kilogramme |
kg |
| volume |
mètre cube |
m3 |
| température |
kelvin |
°K |
| pression
|
pascal |
Pa |
|
énergie |
joule
|
J
|
On utilise également :
- comme unité de pression, le bar = 0.1 Mpa
- comme unité d'énergie, le kilowattheure ( kWh) : 1 kWh = 3600 kJ.
|