|
Série
7:
PUISSANCE, TRAVAIL ET ÉNERGIES
|
EXERCICE
1:
Soit
un champ de force  (M) définit dans un repère
(M) définit dans un repère
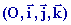 en tout point
en tout point
M(x,
y, z) de l’espace
par :
 =
k (yz – 2xy)
=
k (yz – 2xy)
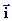 + k (xz – x2)
+ k (xz – x2)
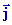 + k xy
+ k xy
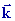 (k
est une constante)
(k
est une constante)
1-
Montrer que cette force dérive d’une énergie potentielle ?
2-
Calculer cette énergie potentielle ?
3-
Calculer le travail de cette force quand son point
d’application se déplace de A(2,1,1)
à B(1,0,2) ?
L’unité
de longueur est le mètre, la force est exprimée en Newton.

EXERCICE
2:
Un point matériel M
de masse m décrit une
trajectoire circulaire (de rayon R
et de centre O) d’un
mouvement à accélération angulaire
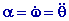 = constante.
= constante.
La position du point M
est repérée dans la base
 des coordonnées polaires.
des coordonnées polaires.
1-
Déterminer le temps que le point matériel mettra pour
atteindre B (q
= p),
sachant qu’à l’instant initial le mobile M
est en A (q
= 0), avec une vitesse nulle ?
2-
En appliquant le principe fondamental de la dynamique, déterminer
dans la base
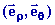 les composantes de la résultante
les composantes de la résultante  à laquelle est soumis
le point matériel M ? à laquelle est soumis
le point matériel M ?
3-
Déterminer le travail WAB
de la force
 , par deux méthodes différentes, en fonction de m,
R et a ?
, par deux méthodes différentes, en fonction de m,
R et a ?
4-
Donner l’expression du moment de la force
 par rapport à O ?
par rapport à O ?
5-
Déterminer le moment cinétique de M
en O. En appliquant
le théorème du moment cinétique, retrouver l’expression
du moment de la force
 par rapport à O ?
par rapport à O ?

EXERCICE
3:
Un point M est mobile sur un cercle de centre O et de rayon
R, repéré par deux axes rectangulaires Ox et Oy. Une force  lui est appliquée, de composantes :
lui est appliquée, de composantes :
X = x + 2y
; Y
= 2x – y
Quel est le travail de
cette force pour un tour complet ? pour chaque demi-tour ?
pour chaque quart de tour ? conclure ?
|