MÉCANIQUE

   EXERCICE 1:    exercice récapitulatif des connaissances.

          Un point matériel M de masse m est repéré dans un référentiel fixe ( Oxyz ) par ses coordonnées cylindriques ( r, q, z ) telles que : r = R ,  q = w t et  z = h q  ( R et w sont des constantes positives et t le temps).

1- Écrire l’expression du vecteur position 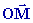 en coordonnées cartésiennes base ( , ,)

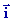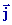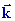2- a) quel est le mouvement du point M dans le plan xOy ?

    b) quel est le mouvement du point M suivant la direction de l’axe Oz ?

    c) quel est le mouvement résultant du point M ?

3- Déterminer les composantes cartésiennes et le module des vecteurs vitesse et accélération ?

4- Calculer l’abscisse curviligne s(t) du point M  sachant qu’à l’instant initial t = 0, s(t) = 0

       5- Quelles sont les composantes tangentielle et normale du vecteur accélération selon les  vecteurs unitaires et du trièdre de Serret- Frenet ?

6- Calculer le rayon de courbure R_C de la trajectoire de M ?

       7- Montrer que la vitesse fait un angle constant a avec l’axe Oz ?, quel est l’hodographe du mouvement ?

8- Quelles sont les coordonnées cylindriques du mouvement du point M ?

9- Déterminer les vecteurs unitaires , et  ?

Réponse: 

1°) En coordonnées cylindriques,
la position du point M est repérée par  r( t ), q = ( t ) et  z ( t ).
Dans la 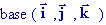,le vecteur position s’écrit : 
= R cos wt + R sin wt + h wt  avec r = R 
2°) 

a – Dans le plan xoy, nous avons : x = R cos wt et y = R sin wt  
avec  x² + y² = R² , c’est un mouvement circulaire de rayon R 
b – Selon la direction de l’axe Oz, on a z = h wt
C’est un mouvement rectiligne uniforme
c – Le mouvement résultant du point M est hélicoïdal simple. La trajectoire est une hélice enroulée sur un cylindre circulaire de rayon R et de pas h constant. 

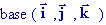3°). La vitesse s’écrit alors dans la sous la forme :

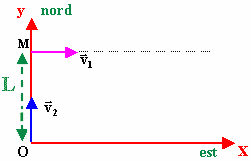
    Un tracteur T et une moissonneuse batteuse M distants de L se trouvent sur un terrain plat. A l’instant initial, le tracteur T se trouve en O pris pour origine, l’axe des ordonnées Oy

 ( orienté vers le nord ) est celui contenant les deux engins et l’axe des abscisses Ox est orienté vers l’est ( voir schéma ).

1- La moissonneuse batteuse M se dirige vers l’est à la vitesse , alors que le tracteur T se dirige vers le nord à la vitesse . Calculer la distance minimale qui va séparer les deux engins ?

2- On suppose que la moissonneuse batteuse se dirige toujours vers l’est à la même vitesse . Déterminer la direction que le tracteur T doit prendre pour rencontrer M dans son parcours ?                                                                          

Calculer le temps nécessaire pour cette rencontre ?