MÉCANIQUE

   EXERCICE 1: 

        Un tracteur tirant une charrue à disque a pour trajectoire la courbe décrite, en coordonnées polaires, par r= r = r₀ e^q  avec une vitesse angulaire w = dq /dt = cte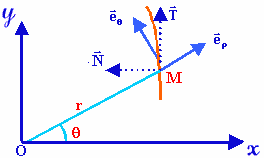
1 - Déterminer dans la base des coordonnées polaires : 
     ¨ les composantes radiale et orthoradiale de la vitesse 
     ¨ les composantes radiale et orthoradiale de l’accélération 

  2 - Calculer la distance parcourue par le tracteur entre l’instant t = 0 et t = 4p/w .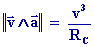

  3 - Déterminer le rayon de courbure de la trajectoire en utilisant la relation  
Comparer cette méthode à celle utilisée dans l’exercice 2 ci-après.
Réponse:  2- s = 2838 m          3-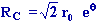

    1°) 
 

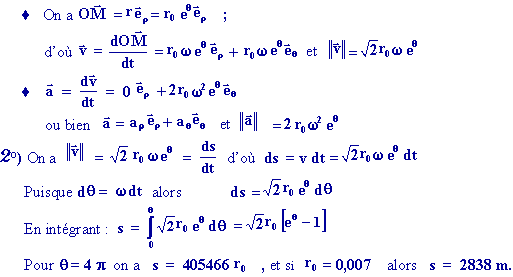
EXERCICE 2:

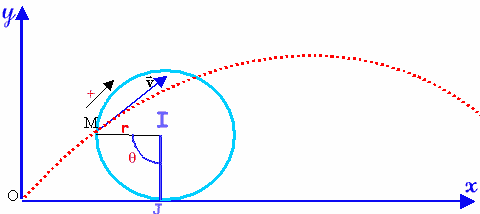
  Supposons qu’un enfant fixe sur la jante de sa bicyclette une orange M qui se déplace dans le plan xoy, nous essayons de suivre sa trajectoire.

 La jante sera considérée comme un cercle de centre I, de rayon r et de vitesse angulaire w  constante. On désigne par J le point de contact du cercle avec OX et par K le point diamétralement opposé. On suppose qu’à l’instant initial le point M du cercle coïncide avec l’origine O.  

  1- quelles sont les coordonnées du point M à l’instant t et la nature de sa trajectoire ?

        (tracer la courbe sur un papier millimétré )

  2- Calculer les coordonnées et le module de la vitesse de M

  3- Donner l’expression de l’abscisse curviligne s(t) pour 0 £ t £ 2p/w  sachant qu’à l’instant initial s(0) = 0 . En déduire la distance parcourue par M quand t = 2p/w.

  4- Calculer les coordonnées et le module de l’accélération de M.

  5- Calculer l’accélération tangentielle et l’accélération normale.

  6- Déterminer le rayon de courbure de la trajectoire au point M.

Réponse:
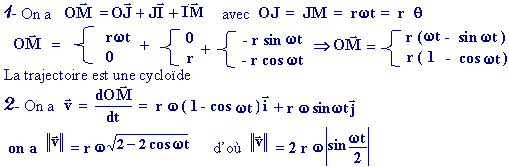