|
Série
10:
FORCES
CENTRALES -
MOUVEMENTS DES PLANÈTES
|
EXERCICE
1:
Un
satellite considéré comme un point matériel M de masse m, décrit
une trajectoire définie en coordonnées polaires par r = f(r)
, sous l’action d’une force centrale
 ,
,
Déterminer l’expression de la force
 si
r = 2 R cos q
(en utilisant la 2ème
formule de Binet ) si
r = 2 R cos q
(en utilisant la 2ème
formule de Binet )
Rappel :
En utilisant les coordonnées polaires (r, q),
les vecteurs vitesse et accélération s’écrivent dans la base
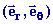 sous la forme suivante :
sous la forme suivante :
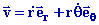 et
et
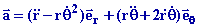
Réponse:

EXERCICE
2:
La
comète de Halley est passée en 1986 au voisinage de la Terre. Sa période
est de 76 années et sa distance minimale ( périgée ) au soleil
est 0.59 u.a ( unité astronomique ).
En utilisant la 3ème
loi de Kepler calculer la plus grande distance ( apogée ) de cette
comète au soleil ainsi que l’excentricité e de sa trajectoire
sans utiliser G ou MS.
Question
supplémentaire : Donner les caractéristiques ( a,
b, c, p, e) de la trajectoire elliptique de la comète de Halley.
Calculer la période de révolution T?

EXERCICE
3:
Un
satellite de la Terre supposé ponctuel de masse m, décrit au tour
de la Terre une trajectoire circulaire de rayon r . On considère
que la Terre est sphérique de rayon R et de masse M et on désigne
par g0 la pesanteur au sol, par h l’altitude et par r =
R + h le rayon de la trajectoire.
1-
Calculer la vitesse v du satellite,
et sa période de révolution T ?
2-
Un autre satellite décrit une
trajectoire de rayon r’ et sa période est T’, exprimer le
rapport des périodes en fonction du rapport des rayons r et r’
(troisième loi de Kepler) ?
3-
Exprimer l’énergie cinétique Ec
, l’énergie potentielle Ep et l’énergie mécanique
Em du satellite en fonction de l’altitude h.
L’énergie potentielle est nulle pour
une altitude infinie.
4- Exprimer la vitesse du satellite en
fonction de l’altitude h ; en déduire la variation de
vitesse en fonction d’une faible variation d’altitude Dh ?
Application
numérique : R =6400
km; h=250 km; Dh=
10 km; g0=9.8 m /s2.


|