|
Série
1:
RAPPELS
MATHÉMATIQUES
|
EXERCICE 1:
Un ingénieur agronome veut déterminer la masse volumique r
d’une pastèque ayant la forme d’une sphère, pour cela :
· Il mesure le diamètre et il trouve 10 cm à 2/10 mm prés.
· Il mesure la masse de la sphère et il trouve m = 3041 g à 1 g prés.
Calculer la valeur de r et déterminer l'incertitude correspondante.
Solution
1
:
Le
volume de la sphère ( pastèque ) est :
V = 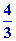 p
R3 p
R3
La
masse volumique est : r
= 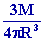 = =
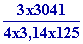 = 5,81 g/cm3
= 5,81 g/cm3
sa
valeur approchée est r
Calcul
de l’incertitude :
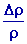 = =
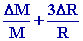  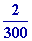
Pour
calculer Dr
on prendra pour r
la valeur simple approchée par excès :r
= 6 g/cm3
D’où
Dr
= 6 x 2/300 = 0,04 g/cm3
et
par suite :
( 5,81 – 0,04 ) g/cm3
£
r
£
( 5,81 +
0,04 ) g/cm3
soit
5,77
g/cm3 £
r
£
5,85
g/cm3
Remarque :
Seul le chiffre 5 est certain.
EXERCICE
2 :
Un topographe effectue le relevé d’un terrain agricole et veut déterminer les coordonnées d’un point M situé à une distance l de l’origine O. On désigne par
a
l’angle formé par 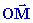 avec l’axe
Ox. avec l’axe
Ox.
1- Déterminer l’abscisse x du point M?
2- Calculer l’erreur relative sur x sachant que :
a- L’erreur commise sur a est négligeable et que l est connue avec une incertitude
Dl
A.N : l = 19,87 m ; Dl = 8 cm
b- L’erreur commise sur l est négligeable et que a est connue avec une incertitude
Da
A.N : a
= 41 ° ; Da = 8’
c- Les incertitudes commises sur l et sur a sont respectivement Dl et
Da .
A.N : l = 19,87 m ;
Dl = 8 cm ;
a
= 41 ° ; Da
= 8’
Solution
2 :
1- On a : x = l cos
a
; A.N : x = 14,99607….m
2-
a- Dx = 0,06
et x = ( 14,99 ± 0,06 ) m
b- Dx = 0,03
et x = ( 14,99 ± 0,03 ) m
c- Dx = 0,09
et x = ( 14,99 ± 0,09 ) m
EXERCICE
3 :
Une parcelle d’un terrain agricole située sur une colline se présente sous forme d’un triangle dont les sommets sont A(1, 1, 0) ; B(0, 2, 4) et C(-1 , -1, 1). ( valeurs
données en centaines de mètres ) .
Déterminer l’aire de la parcelle et exprimer le résultat en hectare ?.
Solution
3 :
Pour calculer l’aire de la parcelle de terrain on écrit :
 = -100 = -100
 + 100
+ 100 + 400 + 400 ; ;
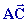 = -200 = -200
 - 200
- 200 + 100 + 100

et  L L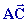 = 90000 = 90000
 -70000
-70000 + 40000 + 40000

la surface du triangle est  ║ ║ L L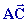 ║= ║=  ( (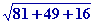 )
104 = 60415 m2 )
104 = 60415 m2
L’aire de la parcelle est égale à : 60415 m2 = 6,0415 hectares
EXERCICE
4 :
Pour déterminer la récolte de blé, un ingénieur dispose d’un silo plein ayant la forme d’un parallélépipède construit sur les points A(1, 0, 0) ; B(0, 1, 1) ; C(4, 2, 0) et
D(5, 3, 4) . ( l’unité est le mètre) .
Déterminer le volume du silo et donner sa valeur approchée si la mesure des dimensions est faite à 0,1 m prés ?.
Solution
4 :
L’ingénieur doit déterminer d’abord :
 = -1
= -1
 + 1
+ 1  +
1
+
1  ; ;
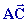 = 3
= 3  2 2
 + 0
+ 0
 et
= 4
et
= 4  3
3
 +
4 +
4  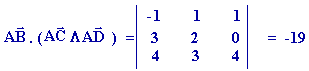
Le volume du silo dont la forme est un parallélépipède construit sur
ces 3 vecteurs, est égal en valeur absolue au produit mixte :
Le volume du silo est 19 m3
EXERCICE
5 :
Un tracteur tire un cover crop en lui appliquant une force
 (2, 1, 1) dont le point d’application est situé en A(0, -1, 1). Calculer le moment de la force (2, 1, 1) dont le point d’application est situé en A(0, -1, 1). Calculer le moment de la force
 par rapport à l’axe ( D) ( supposé confondu avec l’axe des disques suspendus au cover crop) passant par B(1, 1, 0) et ayant pour vecteur unitaire
par rapport à l’axe ( D) ( supposé confondu avec l’axe des disques suspendus au cover crop) passant par B(1, 1, 0) et ayant pour vecteur unitaire
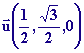
Solution
4 :
Le moment de
 par rapport à l’axe ( D
) est égal à : 1,098 Nm
par rapport à l’axe ( D
) est égal à : 1,098 Nm
|