|
EXERCICE
1:
Soit
un champ de force F(M) défini dans un repère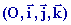 
en tout point M(x
,y ,z ) de l'espace par :
= (-yz-2x)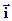 
+ (-xz-4y)  +
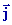(-xy+2z)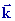 
Calculer
le travail de cette force quand son point d'application se déplace
de A(-1,-2,1) à B(2,3,2) ? .
REMARQUE
IMPORTANTE:
Au
début, vous devez démontrer que (M) dérive d'une énergie
potentielle Ep que vous déterminerez,
ensuite vous calculerez le travail demandé.
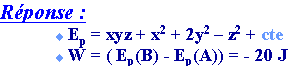
EXERCICE
2:
Une
masse m=10 g, fixée à l'extrémité d'un ressort horizontal de
constante de raideur k = 0,0064 N/cm , se déplace sans frottement
suivant l'axe ox..
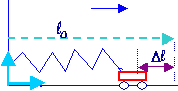
On
suppose qu'à l'instant initial la masse m se trouve en x0= 8 cm avec
une vitesse nulle et qu'au cours
du mouvement elle est soumise à une force extérieure :
2
= 0,01 cos ( wt )
.
Déterminer
l'équation du mouvement de la masse m ? .
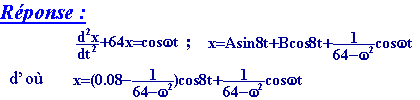
EXERCICE
3:
Trouver
le centre de masse G d'une hémisphère rigide homogène, d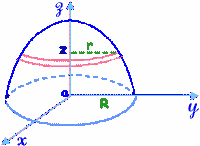e rayon R
et de masse M, représentée sur la figure ?
Déterminer
le moment d'inertie Iox de l'hémisphère par rapport à
l'axe ox? .
RAPPEL:
Le
moment d'inertie d'un disque de rayon r et de masse m par rapport à
son axe de rotation (D)
est ½r²m.
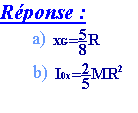
EXERCICE
4:
Un
homme saute d'une hauteur h
= 825 cm. Pendant le saut il tombe verticalement. Il amortit son
arrivée au sol par une flexion de genoux
pendant laquelle l'ensemble (tronc, bras et tête) subit une décélération
constante, puis s'immobilise.
La
distance parcourue par le centre de masse G de cet ensemble pendant
la phase de décélération est
d =755 mm. La masse de cet ensemble est m= 825000 dg, l'accélération
de la pesanteur est g=10
m/s² .
a-
En
déterminant la vitesse de l'homme lorsque ses pieds touchent le sol,
calculer l'accélération
du centre de masse G pendant la phase d'amortissement ? .
b- Calculer
la force exercée par les jambes sur l'ensemble pendant cette phase ?
| 
